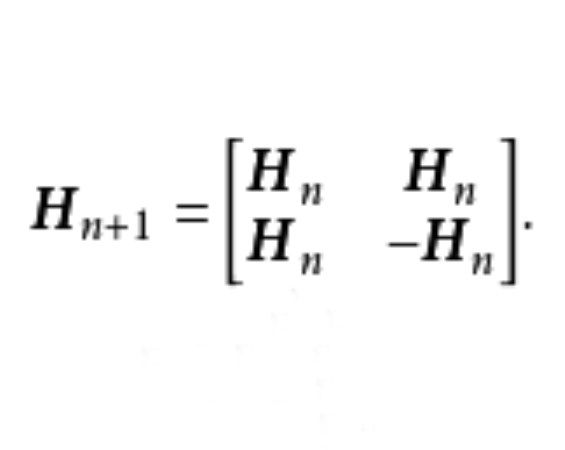阿達馬碼

阿達馬碼(Hadamard code)是一種重要的碼，它是從阿達馬矩陣產生的二元碼，設H_n是一個n階阿達馬矩陣，用0代替H_n與-H_n中的元素-1，這樣可得2n個行，它們都是F₂中的元，由於阿達馬矩陣的任意兩行在一半位置上的元素相異，這2n個向量便構成了一個二元(n，2n，n/2)碼，稱為阿達馬碼。字長為32的阿達馬碼曾被1969年美國發射的航海者號(Mariner)宇宙飛船實際採用，得到了人類從宇宙空間發回的第一張行星照片.從火星及水星等行星拍攝到的每一張黑白照片分成600行600列，共由36萬個點組成，每個點(即一小方格)的明暗程度分為64個等級，由6維的二元向量來表示.經過編碼後每個6維向量變為字長為32的阿達馬碼中的某個碼字，然後發回地面.即使在宇宙空間中因各種干擾使字長為32的碼字發生畸變，但只要發生差錯的位置不超過[(n/2-1)/2]=7個，地面上收到畸變的碼字後仍能正確譯出原來的6維二元向量，1977年發射的旅行者號(Voyager)則採用別的碼發回了彩色的照片。

基本介紹

• 中文名：阿達馬碼
• 外文名：Hadamard code
• 所屬學科：數學（組合設計）
• 簡介：從阿達馬矩陣產生的二元碼

基本介紹

元素為+1或-1的n階方陣H稱為n階阿達馬矩陣，若且唯若HH=nI，換句話說，H是一個正交矩陣，如果H的第一行全為+1，則稱它為規一化的阿達馬矩陣。

n階阿達馬矩陣存在的必要條件是n=1，2或4k。

2階阿達馬矩陣H_n可以按如下方法遞歸地生成：H₀=1，對非負整數n≥0，

將一個規一化的n階阿達馬矩陣中的+1變為0，同時將-1變為1，得到矩陣A稱阿達馬碼，若將A的第一列去掉，便得到一個碼A₁，若將A₁與其互補矩陣重疊，便得到一個碼，若將A與其互補矩陣重疊，便得到一個碼。

只要存在足夠的阿達馬矩陣，那么普洛特金（Plotkin）界是可以達到的。

阿達馬碼的套用

阿達馬矩陣還可在數字通信中用於構造糾錯碼，從阿達馬矩陣產生的糾錯碼稱為阿達馬碼。字長為32的阿達馬碼曾被1969年美國發射的航海者號宇宙飛船實際採用，得到了人類從宇宙空間發回的第1張行星照片，從火星及水星等行星拍攝到的每一張黑白照片分成600行、600列，共由36萬個點組成，每個點(即一小方格)的明暗程度分為64個等級，由6維的二元向量(即每個分量只能取0或1的向量)來表示，經過編碼後每個6維向量變為字長為2=32的阿達馬碼中的某個碼字，然後發回地面，即使在字宙空間中因各種干擾使字長為32的碼字發生畸變，但只要發生差錯的位置不超過7個，地面上收到畸變的碼字後仍能正確譯出原來的6維二元向量，提高了清晰程度，利用阿達馬矩陣還可構造其他類型的碼(如三元自對偶碼)。

相關定理及介紹

Plotkin界

設A(n,d)是(n,d)代碼中代碼字的最大數量，下面的結果給出大多數情況下的一個更好的上界。

定理1(Plotkin)假設(n, d)代碼有N個代碼字，如果，那么

推論2 如果，則

一個秩為4的規範阿達馬矩陣給出一個的(n,d)代碼，且有個代碼字，因此

根據推論2,有

因此，從規範阿達馬矩陣得到的代碼與最佳可能的代碼很接近，根據代碼字的數量，通過加入一個代碼字1...1，我們可以得到最佳可能的代碼，這個字與由阿達馬矩陣所得的任意代碼字的距離是2m，因為任意這樣的代碼字都有2m-1個1和2m個0，因此，我們有4m個字的代碼，其中每一個字的長度是4m-1，而且兩個代碼字之間的最小距離等於2m，這個代碼稱為(4m-1)阿達馬碼。所以有：

等式(1)和不等式(2)給出下面的定理：

定理3 對於存在秩為4m的(規範)阿達馬矩陣的所有m，有：

這個界是通過使用(4m-1)阿達馬碼得到的。

設B(n，d)是長度為n的字的最大數量，其中每一個字與其他字之間的距離都正好是d，顯然，B(n，d)≤A(n, d)。

推論4對於存在秩為4m的規範阿達馬矩陣的所有m，有

證明：我們已構造的代碼字都有距離2m。

注意，有趣的是，有時可以通過把代碼字的長度增加1而得到豐富得多的代碼，我們將證明下面的定理。

定理5 對於存在秩為4m的規範阿達馬矩陣的所有m，有

這一定理表明， 在存在秩為4m的(規範)阿達馬矩陣的情況下，加入一個數字導致可能的代碼字數量成倍增加一倍。

定理6如果，那么

(4m)阿達馬碼還稱為(第一類) Reed-Muller碼， 這是以Reed和Muller的名字命名的，定理3和定理5的結果歸功於Levenshtein，他還得到了更一般的結果。