阿達馬三圓定理

阿達馬三圓定理是一個關於全純函式性質的結論。即：設f(z)是環域 上的全純函式，M(r)是|f(z)|在圓周|z|=r上的最大值。那么，logM(r)是一個對數log(r)的凸函式。

基本介紹

• 中文名：阿達馬三圓定理
• 外文名：Hadamard，Jacques-Salomon
• 提出者：雅克·所羅門·阿達馬
• 套用學科：數學
• 適用領域範圍：同心圓
• 適用領域範圍：複分析

簡介

阿達馬三圓定理是關於圓環內解析函式在圓環的同心圓周上的最大模的增長性定理。

定義

設 f(z) 是環域 上的全純函式， M(r) 是 | f(z) | 在圓周 | z | = r 上的最大值。那么， logM(r) 是一個對數 log(r) 的凸函式。進一步，如果不存在常數 λ 和c，使得 f(z) 是 cz 的形式，那么 logM(r) 是 log(r) 的嚴格凸函式。

定理結論可以重述為：

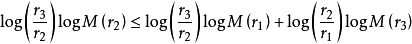
對任何半徑為 r₁ < r₂ < r₃ 的同心圓成立。

推導

阿達馬三圓定理 在複分析中，阿達馬三圓定理是一 個關於全純函式性質的結論。 設 f(z) 是環域 上的全純函 數， M(r) 是 | f(z) | 在圓周 | z | = r 上的最大值。那么， logM(r) 是 一個對數 log(r) 的凸函式。 進一步， 如果不存在常數 λ 和 c，使得 f(z) 是 cz 的形式，那么 logM(r) 是 log(r) 的嚴格凸函式。

定理結論可以重述為： 對任何半徑為r₁<r₂<r₃的同心圓成立。