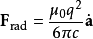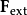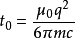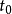阿布拉罕-勞侖茲力

阿布拉罕-洛倫茲力（Abraham-Lorentz force）是一加速帶電粒子因為粒子放射出電磁輻射而所受到的平均力。其適用在粒子行進速度不快的時候。若在相對論性速度下，此力則稱作是阿布拉罕-洛倫茲-狄拉克力（Abraham-Lorentz-Dirac force）。

基本介紹

• 中文名：阿布拉罕-勞侖茲力
• 外文名：Abraham-Lorentz force

簡介

阿布拉罕-洛倫茲力問題的解被認為預測了“來自於未來的訊號影響了現在”這樣的結果，而挑戰了直觀上的因果律。試圖解決此一問題的涉及到許多近代物理的領域，雖然Yaghjian曾展試過這問題的解實際上相當簡單。

定義與描述

數學上，阿布拉罕-洛倫茲力可寫為：

（SI單位制）

（cgs單位制）

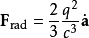
其中：

F是力，

是加加速度（加速度的時間導數）。

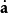
μ₀和ε₀是真空磁導率和真空電容率，

c是真空中的光速，

q是電荷量。

當速度很慢時。根據拉莫爾方程，一加速電荷放出輻射，而輻射會將動量自電荷帶走。既然動量是守恆的，電荷會被推往與輻射釋放方向相反的方向。阿布拉罕-洛倫茲力即為因於輻射釋放而施加在一加速電荷上的平均力。

背景

經典電動力學中，問題通常可以分為兩類：

1. 問題中，產生場的電荷與電流源已指定，要計算出場；
   
2. 問題中，場已指定，要計算出電荷的運動。
   

在一些物理學領域中，如電漿物理學，場由源產生，而源的運動可以自洽的解出。然而在這樣的場合中，源的運動常是從所有其他的源產生的場來計算。很少去計算一粒子（源）所產生的場，對於同一粒子造成什麼樣的運動影響。理由有兩個層次：

1. 忽略“自身場（self-fields）”通常仍可得到足夠精確的答案，足以用在許多套用上；
   
2. 包含自身場會導致物理學中未解決的問題，關係到物質與能量的本質。
   

由自身場所衍生的概念問題在標準的研究生教科書有所著墨。（Jackson電動力學）

（譯自原文）此一問題所引出的困難涉及到物理學中最重要的基本面貌之一──基本粒子的本質。雖然在一些設有限制的領域中，有部分可用的解已經給出，然則基本問題方面則仍舊未有解決。一些人可能希望從經典到量子處理方法上的過渡可以解決這樣的難題。雖仍希望這件事終究會發生，不過當前量子力學方面的討論甚至還遇上了比經典還要複雜得多的狀況。在較近期的年代中（~ 1948年 - 1950年），所出現的成就之一是將洛倫茲協變性與規範不變性等概念巧妙地運用，在量子電動力學中迴避了這些困難，而允許對於非常小的輻射效應做出計算，達到極高的精準度，並與實驗結果相符。但若從基本觀點來看，這樣的難題依舊是存在的。

推導

我們從點電荷輻射的拉莫爾方程開始：

如果我們假設帶電粒子的運動是周期性的，則阿布拉罕-洛倫茲力對粒子所做的功等於拉莫功率從 到 的積分：

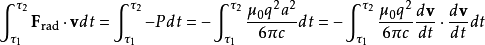
我們可以用分部積分法來計算以上的積分。如果我們假設運動是周期性的，則表達式的第一項為零：

因此，我們有：

來自未來的訊號

下面展示了一種會導致驚人結果的經典分析方法。可以看到，經典理論正在挑戰因果律的標準圖景，表明要么因果律被破壞，要么理論需要擴展。在本例中，理論的擴展包括量子力學和它的相對論版本量子場論。參考Rohrlich關於“物理學理論遵循有效性限制的重要性”的介紹。

對於一個受到外力 ，我們有

其中：

公式經過整理後，可以得到：

這個積分從當前延續到無窮遠的未來。因而未來的作用力將影響到粒子當前的加速度。未來的數值按以下因子加權：

隨著未來超過 時間的增長而迅速減小。因此，大概在未來時間段內的信號會影響到當前的加速度。對於電子來說，這個時間段大約是 秒，相當於光線穿越電子“尺寸”所需的時間。