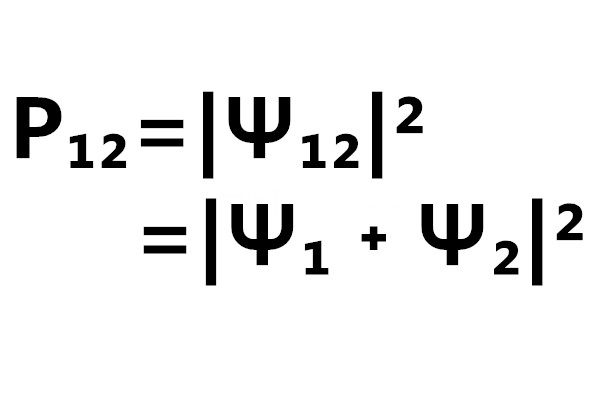基本介紹
- 中文名:機率幅
- 外文名:probability amplitude
- 別名:量子幅
- 性質:複函數
- 所屬領域:數理科學
- 相關人物:德布羅意、玻恩、薛丁格、費恩曼
研究背景,詳細定義,
研究背景
德布羅意提出的波的物理意義是什麼呢?他本人曾認為那種與粒子相聯繫的波是引導粒子運動的“導波”,並由此預言了電子的雙縫干涉的實驗結果。這種波以相速度u=c2/v傳播而其群速度就正好是粒子運動的速度u。對這種波的本質是什麼,他並沒有給出明確的回答,只是說它是虛擬的和非物質的。
量子力學的創始人之一薛丁格在1926年曾說過,電子的德布羅意波描述了電量在空間的連續分布。為了解釋電子是粒子的事實,他認為電子是許多波合成的波包。這種說法很快就被否定了。因為。第一,波包總是要發散而解體的,這和電子的穩定性相矛盾;第二.電子在原子散射過程中仍保持穩定也很難用波包來說明。
當前得到公認的關於德布羅意波的實質的解釋是玻恩(M.Born)在1926年提出的。在玻恩之前,愛因斯坦談及他本人論述的光子和電磁波的關係時曾提出電磁場是一種“鬼場”。這種場引導光子的運動,而各處電磁波振幅的平方決定在各處的單位體積內一個光子存在的機率。玻恩發展了愛因斯坦的思想。他保留了粒子的微粒性,而認為物質波描述了粒子在各處被發現的機率。這就是說,德布羅意波是機率波。
 圖1
圖1玻恩的機率波概念可以用電子雙縫衍射的實驗結果來說明。圖1(a)的電子雙縫衍射圖樣和光的雙縫衍射圖樣完全一樣,顯示不出粒子性,更沒有什麼機率那樣的不確定特徵。但那是用大量的電子(或光子)做出的實驗結果。如果減弱入射電子束的強度以致使一個一個電子依次通過雙縫,則隨著電子數的積累,衍射“圖樣”將依次如圖2中各圖所示。圖(a)是只有一個電子穿過雙縫所形成的圖像。圖(b)是幾個電子穿過後形成的圖像。圖(c)是幾十個電子穿過後形成的圖像。這幾幅圖像說明電子確是粒子.因為圖像是由點組成的。它們同時也說明.電子的去向是完全不確定的.一個電子到達何處完全是機率事件。隨著入射電子總數的增多,衍射圖樣依次如(d).(e),(f)諸圖所示,電子的堆積情況逐漸顯示出了條紋,最後就呈現明晰的衍射條紋,這條紋和大量電子短時問內通過雙縫後形成的條紋(圖1(a))一樣。這些條紋把單個電子的機率行為完全淹沒了。這又說明.儘管單個電子的去向是機率性的,但其機率在一定條件(如雙縫)下還是有確定的規律的。這些就是玻恩機率波概念的核心。
圖2表示的實驗結果明確地說明了物質波並不是經典的波。經典的波是一種運動形式。在雙縫實驗中,不管人射波強度如何小,經典的波在縫後的屏上都“應該”顯示出強弱連續分布的衍射條紋.只是亮度微弱而已。但圖2明確地顯示物質波的主體仍是粒子,而且該種粒子的運動並不具有經典的振動形式。
 圖2
圖2圖2表示的實驗結果也說明微觀粒子並不是經典的粒子。在雙縫實驗中,大量電子形成的衍射圖樣是若干條強度大致相同的較窄的條紋。如圖3(a)所示。如果只開一條縫,另一條縫閉合,則會形成單縫衍射條紋。其特徵是幾乎只有強度較大的較寬的中央明紋(圖3(b)中的P1和P2)。如果先開縫1,同時關閉縫2,經過一段H寸間後改開縫2。同時關閉縫1,這樣做實驗的結果所形成的總的衍射圖樣P12將是兩次單縫衍射圖樣的疊加.
其強度分布和同時打開兩縫時的雙縫衍射圖樣是截然不同的。
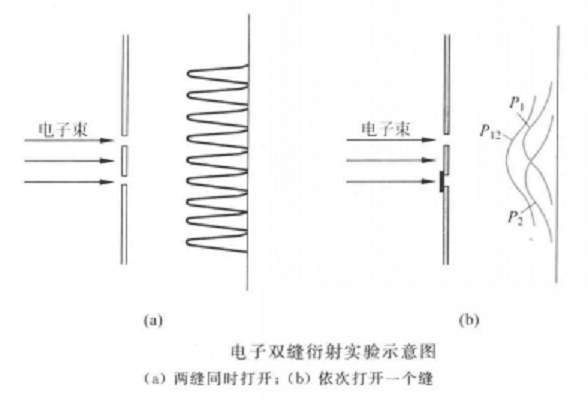 圖3
圖3如果是經典的粒子.它們通過雙縫時.都各自有確定的軌道,不是通過縫1就是通過縫2。通過縫l的那些粒子,如果也能衍射的話,將形成單縫衍射圖樣。通過縫2的那些粒子.將形成另一幅單縫衍射圖樣。不管是兩縫同時開,還是依次只開一個縫,最後形成的衍射條紋都應該是圖3(b)那樣的兩個單縫衍射圖樣的疊加。實驗結果顯示實際的微觀粒子的表現並不是這樣。這就說明,微觀粒子並不是經典的粒子。在只開一條縫時,實際粒子形成單縫衍射圖樣。在兩縫同時打開時,實際粒子的運動就有兩種可能:或是通過縫1或是通過縫2。如果還按經典粒子構想,為了解釋雙縫衍射圖樣,就必須認為通過這個縫時,它好像“知道”另一個縫也在開著,於是就按雙縫條件下的機率來行動了。這種說法只是一種“擬人”的想像,實際上不可能從實驗上測知某個微觀粒子“到底”是通過了哪個縫,我們只能說它通過雙縫時有兩種可能。微觀粒子由於其波動性而表現得如此不可思議地奇特!但客觀事實的確就是這樣!
詳細定義
為了定量地描述微觀粒子的狀態,量子力學中引入了波函式,並用Ψ表示。一般來講,波函式是空間和時間的函式,並且是複函數,即Ψ=Ψ(x,y,z,t)。將愛因斯坦的“鬼場”和光子存在的機率之間的關係加以推廣,玻恩假定|Ψ|2=ΨΨ*就是粒子的機率密度,即在時刻t.在點(x,y,z)附近單位體積內發現粒子的機率。波函式Ψ因此就稱為機率幅。對雙縫實驗來說,以Ψ1表示單開縫1時粒子在底板附近的機率幅分布,則|Ψ1|2=P1即粒子在底板上的機率分布,它對應於單縫衍射圖樣P1(圖3(b))。以Ψ2表示單開縫2時的機率幅,則|Ψ2|2=P2表示粒子此時在底板上的機率分布,它對應於單縫衍射圖樣P2.如果兩縫同時打開,經典機率理論給出,這時底板上粒子的機率分布應為
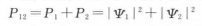 4
4但事實不是這樣!兩縫同開時.入射的每個粒子的去向有兩種可能,它們可以“任意”通過其中的一條縫。這時不是機率相疊加.而是機率幅疊加,即相應的機率分布為
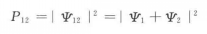 5
5這裡最後的結果就會出現Ψ1和Ψ2的交叉項。正是這交叉項給出了兩縫之間的干涉效果,使雙縫同開和兩縫依次單開的兩種條件下的衍射圖樣不同。
機率幅疊加這樣的奇特規律,被費恩曼(R.P.Feynman)在他的著名的《費恩曼物理學講義》中稱為“量子力學的第一原理”。他這樣寫道:“如果一個事件可能以幾種方式實現,則該事件的機率幅就是各種方式單獨實現時的機率幅之和。於是出現了干涉。”
在物理理論中引人機率概念在哲學上有重要的意義。它意味著:在已知給定條件下,不可能精確地預知結果,只能預言某些可能的結果的機率。這也就是說,不能給出唯一的肯定結果,只能用統計方法給出結論。這一理論是和經典物理的嚴格因果律直接矛盾的。玻恩在1926年曾說過:“粒子的運動遵守機率定律,但機率本身還是受因果律支配的。”這句話雖然以某種方式使因果律保持有效,但機率概念的引入在人們了解自然的過程中還是一個非常大的轉變。因此,儘管所有物理學家都承認,由於量子力學預言的結果和實驗異常精確地相符,所以它是一個很成功的理論,但是關於量子力學的哲學基礎仍然有很大的爭論。哥本哈根學派,包括玻恩、海森伯(W.Heisenberg)等量子力學大師,堅持波函式的機率或統計解釋,認為它就表明了自然界的最終實質。費恩曼也寫過(1965年):“現時我們限於計算機率。我們說‘現時’,但是我們強烈地期望將永遠是這樣一解除這一困惑是不可能的自然界就是按這樣的方式行事的。”
另一些人不同意這樣的結論,最主要的反對者是愛因斯坦。他在1927年就說過:“上帝並不是跟宇宙玩擲骰子遊戲。”德布羅意的話(1957年)更發人深思。他認為:不確定性是物理實質,這樣的主張“並不是完全站得住的。將來對物理實在的認識達到一個更深的層次時,我們可能對機率定律和量子力學作出新的解釋,即它們是目前我們尚未發現的那些變數的完全確定的數值演變的結果。我們現在開始用來擊碎原子核並產生新粒子的強有力的方法可能有一天向我們揭示關於這一更深層次的目前我們還不知道的知識。阻止對量子力學目前的觀點作進一步探索的嘗試對科學發展來說是非常危險的,而且它也背離了我們從科學史中得到的教訓。實際上,科學史告訴我們,已獲得的知識常常是暫時的.在這些知識之外,肯定有更廣闊的新領域有待探索。”最後,還可以引述一段量子力學大師狄拉克(P.A.M.Dirac)在1972年的一段話:“在我看來,我們還沒有量子力學的基本定律。目前還在使用的定律需要作重要的修改,……。當我們作出這樣劇烈的修改後.當然.我們用統計計算對理論作出物理解釋的觀念可能會被徹底地改變。”