由增量調製原理可知,解碼器恢復的信號是階梯形電壓經過低通濾波器平滑後的解調電壓。它與編碼器輸入模擬信號的波形近似,但是存在失真,將這種失真稱為量化噪聲。
基本介紹
- 中文名:量化噪聲
- 外文名:quantization noise
定義,產生原因,實際套用,量化噪聲計算,信號量噪比,
定義
在語言編碼通信中,解調後信號和原傳遞信號的差異是因幅度和時間的量化而產生的,這種失真稱為量化失 真。因為這種失真和雜亂的干擾一樣,聽起來和元件產生的熱噪聲相似,所以叫做量化噪聲。
產生原因
(1)第一個原因是由於編碼、解碼時用階梯波形去近似表示模擬信號波形,由於階梯本身的電壓突跳產生失真。如下圖(a),這是增量調製的基本量化噪聲,又稱一般量化噪聲。它伴隨著信號永遠存在,即只要有信號,就有這種噪聲。
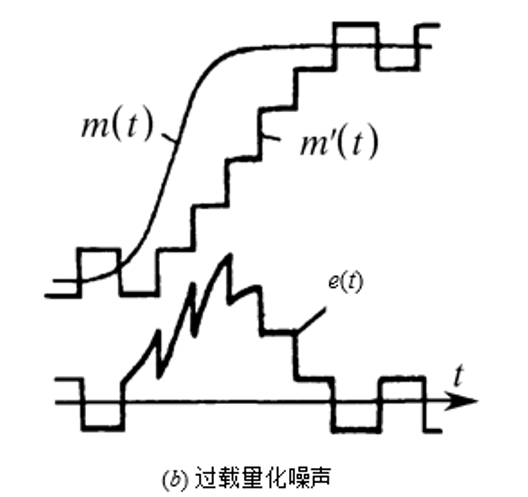
(2)第二個原因是信號變化過快引起失真,這種失真稱為過載量化噪聲,見下圖(b),它發生在輸入信號斜率的絕對值過大時,由於當抽樣頻率和量化台階一定時,階梯波的最大可能斜率是一定的。若信號上升的斜率超過階梯波的最大可能斜率,則階梯波的上升速度趕不上信號的上升速度,就發生了過載量化噪聲。

設抽樣周期為 ,抽樣頻率為
,抽樣頻率為 ,量化台階為
,量化台階為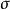 ,則一個階梯台階的斜率
,則一個階梯台階的斜率 為
為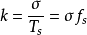
 ,
,


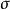

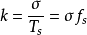

它也就是階梯波的最大可能斜率,或稱為解碼器的最大跟蹤斜率。當增量調製器的輸入信號斜率超過這個最大值時,將發生過載量化噪聲。所以,為了避免發生過載量化噪聲,必須使 和
和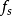 的乘積足夠大,使信號的斜率不會超過這個值。另一方面,
的乘積足夠大,使信號的斜率不會超過這個值。另一方面,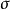 值直接和基本量化噪聲的大小有關,若取
值直接和基本量化噪聲的大小有關,若取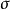 值太大,勢必增大基本量化噪聲。所以,用增大
值太大,勢必增大基本量化噪聲。所以,用增大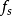 的辦法增大乘積
的辦法增大乘積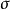
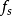 ,才能保證基本量化噪聲和過載量化噪聲兩者都不超過要求。
,才能保證基本量化噪聲和過載量化噪聲兩者都不超過要求。

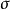
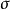
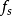
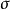
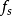
實際套用
量化噪聲計算
這是僅考慮基本量化噪聲,並假定在設計時已經考慮到使系統不會產生過載量化噪聲,這樣模擬信號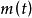 與預測信號
與預測信號 之差就是低通濾波前的量化噪聲
之差就是低通濾波前的量化噪聲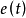 。有上圖(a)可知,
。有上圖(a)可知,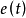 隨時間在區間
隨時間在區間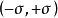 內變化。假設它在此區間內均勻分布,則
內變化。假設它在此區間內均勻分布,則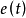 的機率分布密度為
的機率分布密度為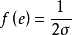
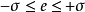
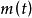

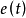
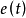
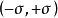
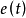
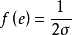
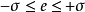
故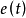 的平均功率可以表示成:
的平均功率可以表示成:
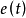

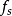

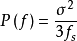
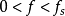
因此,此量化噪聲通過截止頻率為 的低通濾波器之後,其功率
的低通濾波器之後,其功率

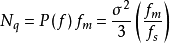


信號量噪比
設輸入信號為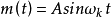 ,式中:A為振幅,
,式中:A為振幅,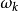 為角頻率。
為角頻率。
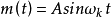
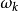
則斜率由下式決定:
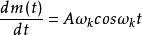
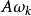
為了保證不過載,要求信號的最大斜率不超過解碼器的最大跟蹤斜率。現在信號的最大斜率為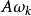 ,所以要求
,所以要求
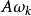





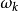

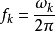
因此,可以求出最大信號量噪比:

