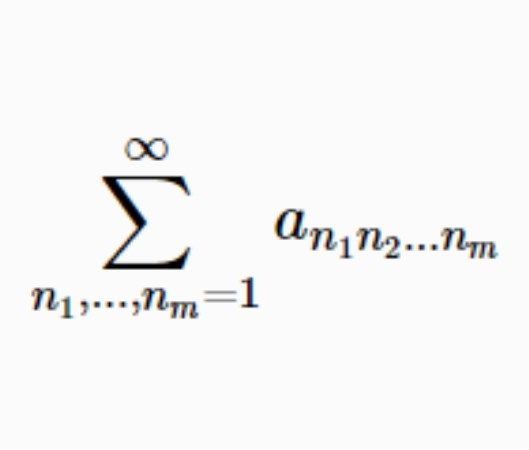基本介紹
- 中文名:重級數
- 外文名:multiple series
- 所屬學科:高等數學
- 別名:多重級數,k重級數
- 簡介:重序列的形式和
基本介紹,相關性質定理,
基本介紹
重級數(1)由m重序列an1n2…nm構成的形如

(2)設(xs)s∈ Np是G之元素的多重序列,對N的任一有限子集J,假定

相關性質定理
設有r個下標 的無窮數組
的無窮數組





多重級數的理論可效仿下面的二重級數理論加以推廣得到。
二重級數是二重序列的形式和,設{amn}是二重序列,把它的項按任意次序排列並以加號連結得到的表達式稱為二重級數,記為

這裡m,n各自獨立地取正整數1,2,3,…數
Smn= aij
aij

稱為(1)的部分和,若二重極限

則稱該二重級數收斂,S為它的和,記為
S= .
.

當這樣的S不存在時,稱這個二重級數發散。若

收斂,則稱(1)絕對收斂。類似於通常的級數(相對於二重級數,通常的級數稱為單級數),可定義二重級數的條件收斂性。單級數的一些基本性質仍為二重級數所保持。例如,非負項二重級數收斂若且唯若其部分和有界,二重級數收斂的必要條件是amn→0(m,n→∞),絕對收斂的二重級數必收斂(參見“絕對收斂級數”)等,對二重函式項級數,也可如函式項級數那樣引進一致收斂概念,並得到相應的柯西準則、M判別法等,設φ是正整數集N+到N+×N+上的一一對應,則對二重級數(1),可以得到級數

φ稱為二重序列{amn}到序列{aφ(k)}k=1的重排,或二重級數(1)到單級數∑aφ(k)的重排.若級數




之一收斂,則:
1.另三個也收斂,且它們的和相等(設為S)。
2. amn與
amn與 amn均絕對收斂於S(
amn均絕對收斂於S( amn與
amn與 amn也絕對收斂)。
amn也絕對收斂)。




在一些文獻中,上述結論被稱為主要重排定理。由此可知,絕對收斂的二重級數的兩個疊級數也絕對收斂,有同一個和。由於二重級數的項的排列次序不惟一以及多種研究目的,因此,還有多種定義二重級數的部分和的方式,相應地也就有了不同的定義二重級數的和與收斂性的方式。