基本介紹
- 中文名:希爾伯特不等式
- 外文名:Hilbert inequality
- 所屬學科:數學
- 提出者:希爾伯特(D.Hilbert)
- 提出時間:1888年
- 簡介:有關雙指標和或重級數的不等式
基本介紹












相關定理


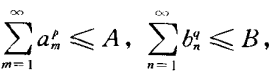






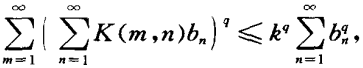


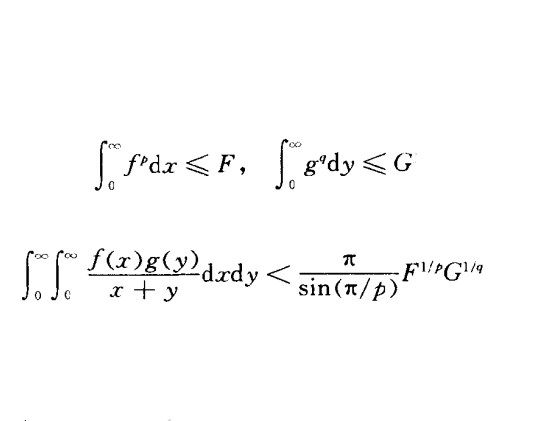














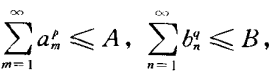






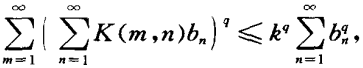


希爾伯特不等式(Hilbert inequality)是有關雙指標和或重級數的一種不等式及其推廣,它是希爾伯特(D.Hilbert)於1888年提出的,關於有限和的不等式。基本介紹希爾伯特不等式是有關雙指標和或重級數的一...
1.1 希爾伯特型不等式的百年回顧 1.2 希爾伯特型不等式的近代研究 第二章 級數求和與歐拉-麥克勞林公式的改進套用 2.1 從一類正項級數的估值方法談起 2.2 伯努利數與伯努利多項式 2.3 伯努利函式 2.4 ...
波利亞合著的一部經典之作,作者詳盡地討論了分析中常用的一些不等式,涉及初等平均值、任意函式的平均值和凸函式理論、微積分的各種套用、無窮級數、積分、變數積分的一些套用、關於雙線性形式和多線性形式的一些定理、希爾伯特不等式及其...
《運算元範數與Hilbert型不等式》是2009年科學出版社出版的圖書,作者是楊必成。內容簡介 《運算元範數與Hilbert型不等式》作者套用實分析、泛函分析中的思想與不等式的權係數及參量化方法,在多類賦范線性空間建立核為負數齊次的Hilbert型不...
對於一個希爾伯特空間中的向量來說,它在任意一個正交序列上的投影的平方和也是小於等於它自身的長度的平方。這就是貝塞爾不等式。貝塞爾不等式的等號成立若且唯若正交序列是完全序列。這時貝塞爾不等式轉化為帕塞瓦爾定理。定理的敘述 設 ...
《正運算元理論》是2009年科學出版社出版的圖書。Hilbert空間上正運算元理論是線性代數中正定矩陣理論向無窮維情形的推廣,《正運算元理論》介紹利用運算元極分解理論研究Hilbert空間上正運算元的若干性質,如不等式的保序性、運算元函式的單調性和若干新...
里斯-菲舍爾定理是貝塞爾不等式的逆命題。設 是希爾伯特空間H中的規範正交系,F張成的閉子空間為E;又設 是一族數,滿足 則必存在惟一的向量x∈E,使x關於{e}的傅立葉係數是{c},即c=(x,e),且 這一結論通常稱為里斯-...
尋找這樣的n是一個很困難的問題, 人們叫做“有效性問題”。它和黎曼洛赫定理、消失定理(也稱消滅定理,淹沒定理)、秩2向量叢、Bogomolov不等式、希爾伯特不變數理論、典範環、極小模型等等有著千絲萬縷的關係。在X是代數曲線的時候,...
