鄰餘角

鄰餘角(adjacent complementary angles)是指與一銳角有特殊關係的角，當兩個鄰角合成直角，即兩條非公共邊互相垂直時，這兩個鄰角則稱互為鄰餘角。同角或等角的鄰餘角相等。

基本介紹

• 中文名：鄰餘角
• 外文名：adjacent complementary angles
• 所屬學科：數學
• 所屬問題：平面幾何（角）
• 性質：同角或等角的鄰餘角相等

基本概念

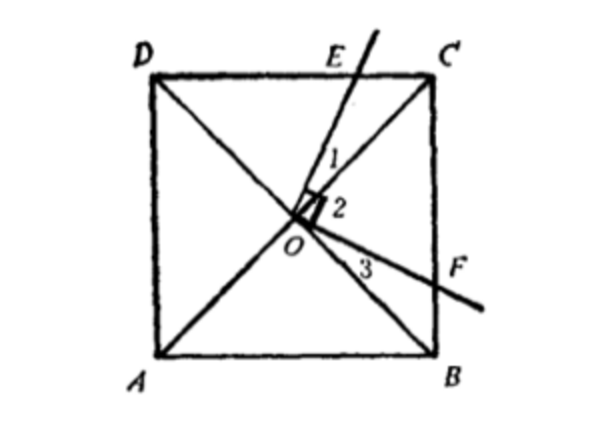
如果兩個角的項點相重合，它們的一條邊也重合，並且這兩個角的另一邊互相垂直，此時稱其中一個角為另一個角的鄰餘角。如圖1中∠1、∠2互為鄰餘角，∠2、∠3互為鄰餘角；如圖2（a）中∠1、∠2互為鄰餘角。

【例1】 如圖1，已知:正方形ABCD對角線交於O點，引射線OE、OF，使∠EOF=90°，OE交CD於E，OF交BC於F，求證：OE=OF。

圖1

分析由題意，∠1、∠2互為鄰餘角，∠2、∠3互為鄰餘角，所以∠1+∠2=90°，∠2+∠3=90°，則∠1=∠3，結合正方形性質易證：△OCE≌△OBF，得OF=OF。

相關概念

定義 如果兩個角的和等於一個直角，這兩個角叫做互為餘角。

例如：∠A+∠B=90°，則∠A是∠B的餘角，∠B是∠A的餘角。

定義 如果兩個角的和等於一個平角，這兩個角叫做互為補角。

例如：∠A+∠B=90°，則∠A是∠B的補角，∠B是∠A的補角。

定義 如果互為鄰角的兩個角又互為餘角，這兩個角叫做鄰餘角。

例如：∠AOB+∠BOC= 90°，則∠AOB與∠BOC互為鄰餘角，見下圖。

定義 如果互為鄰角的兩個角又互為補角，這兩個角叫做鄰補角。

例如：∠AOB+∠BOC=180°，則∠AOB與∠BOC互為鄰補角。

鄰餘角

鄰補角

五種互余

下面分五種情況來研究兩個銳角互余。

基本圖五——1的條件是鄰餘角。

圖2（a）

基本圖五——2的條件是直角三角形中兩銳角互余。

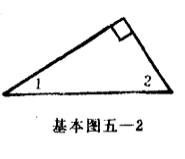圖2（b）

基本圖五——3是， 過直角頂點另作一條直線，也就是一個平角被分成三部分，中間是直角，那么兩側的兩個銳角互余。

圖2（c）

基本圖五——4是一個四邊形，有一組對角分別是直角，那么另一組對角之和為180°。這組互補的角各自作出角平分線，就有兩組角分別相等，分別從每組中任取一個角，則互為餘角。

圖2（d）

基本圖五——5是平行線同旁內角的平分線，將互補的兩個角各自平分，從每組各取一一個角， 則互為餘角，從而這兩條角平分線相交成直角。這個圖形在圓的切線時也會用到它。例如⊙O有兩條平行切線，過半圓上任意一點再作一條⊙O的切線，它們兩兩相交，仍然出現這個圖形。

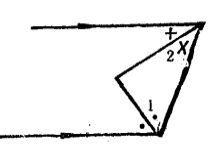圖2（e）