基本介紹
- 中文名:邊角邊公理
- 外文名:Edge and side axioms
- 學科:數理科學
- 類型:數學術語
- 用途:證明兩個三角形全等
- 簡稱:SAS
三角形
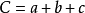
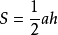
全等三角形
簡介
性質
概念
相關教學
教學內容
教學目標
重點、難點與關鍵
教學方法
證明方法
例題
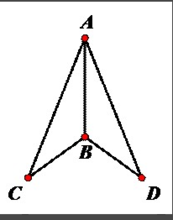
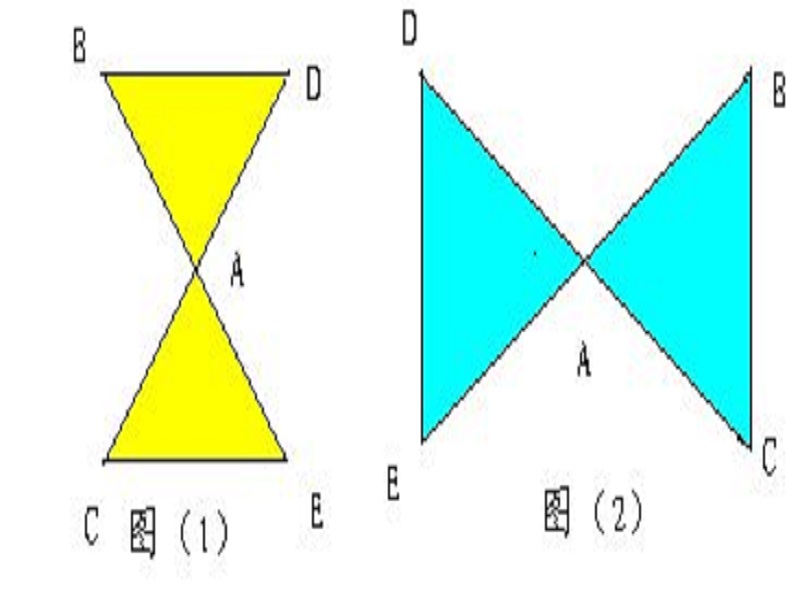
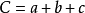
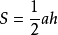

邊角邊公理是兩邊和它們夾角對應相等的兩個三角形全等。經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形,邊角邊公理是判斷兩個三角形全等的重要公理之一...
角邊角公理(ASA):兩個三角形對應的兩角及其夾邊相等,兩個三角形全等。經過翻轉、平移後,能夠完全重合的兩個三角形叫做全等三角形,角邊角公理是證明是兩三角形...
概念角角邊公理是角邊角公理的一種延伸。 兩個角和其中一個角的對邊對應相等的兩個三角形全等(可以簡寫成“角角邊”或“AAS”).公理證明首先,Δ ABC與Δ A...
全等三角形定理 角角邊公理:兩角和其中一角的對邊對應相等的兩個三角形全等。簡寫成“角角邊”或“AAS"此外,全等三角形判定定理還有"邊邊邊”(sss) “邊角邊...
邊角邊公理(SAS):各三角形的其中兩條邊的長度都對應相等,且這兩條邊的夾角(即這兩條邊組成的角)都對應相等的話,該兩個三角形就是全等三角形。...
22邊角邊公理(sas) 有兩邊和它們的夾角對應相等的兩個三角形全等23 角邊角公理( asa)有兩角和它們的夾邊對應相等的兩個三角形全等...
21 全等三角形的對應邊、對應角相等22邊角邊公理(sas) 有兩邊和它們的夾角對應相等的兩個三角形全等23 角邊角公理( asa)有兩角和它們的夾邊對應相等的兩個...
24 推論(AAS) 有兩角和其中一角的對邊對應相等的兩個三角形全等 25 邊邊邊公理(SSS) 有三邊對應相等的兩個三角形全等 26斜邊、直角邊公理(HL) 有斜邊和一...
21.全等三角形的對應邊、對應角相等22.邊角邊公理(SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等23.角邊角公理(ASA)有兩角和它們的夾邊對應相等的兩個...
邊角邊公理 角邊角公理 邊邊邊定理 軸對稱圖形 第四比例項外角平分線 相似多邊形 內接四邊形 相似三角形 內接三角形內接多邊形 內接五邊形 外切三角形 外切...
21 全等三角形的對應邊、對應角相等22邊角邊公理(SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等23 角邊角公理( ASA)有兩角和它們的夾邊對應相等的兩個...
21 、全等三角形的對應邊、對應角相等22、邊角邊公理(SAS) 有兩邊和它們的夾角對應相等的兩個三角形全等23 、角邊角公理( ASA)有兩角和它們的夾邊對應相等的...
26 斜邊、直角邊公理(hl) 有斜邊和一條直角邊對應相等的兩個直角三角形全等27 定理1 在角的平分線上的點到這個角的兩邊的距離相等...
