基本介紹
- 中文名:遭遇角
- 外文名:Encounter angle
- 描述:船首與波浪前進方向之間的夾角
- 套用:船舶
- 學科:船舶工程
概念,船舶遭遇角頻率的估算,船舶橫搖數據的獲取,譜估計,仿真驗證,研究結論,基於遭遇角決策的並行雙模切換舵減搖控制,並行雙模轉換控制方案,遭遇角自動判斷,研究結論,
概念
遭遇角是指船首前進的方向與波浪前進方向之間的夾角。遭遇角頻率對船舶的航行安全和減搖效果都是至關重要的。然而,船舶操縱者無法直接預報出船舶的遭遇角頻率,這對研究船舶在海浪中的運動造成了不便。為了解決上述問題,相關研究首先在特定海況下,通過海浪理論和Conolly理論建立海浪的波傾角模型和船舶的橫搖運動模型,仿真出船舶的橫搖歷程,然後套用Welch譜估計方法估算船舶的橫搖角譜,進而求取船舶發生最大諧振時的遭遇角頻率,最後把估算出的遭遇角頻率與理論上計算出來的船舶最大諧振的遭遇角頻率進行比較分析,以驗證該方法的有效性。
船舶遭遇角頻率的估算
船舶在海平面上行駛時,不可避免地會受到海洋環境的擾動使其運動姿態發生變化,其中在船舶遭受的所有擾動中,海浪對其造成的影響最大,由於船舶的遭遇角頻率是船舶遭受到海浪的擾動後做出回響的頻率,故它反應了船舶是如何遇上影響其運動的波浪的,因此估算遭遇角頻率對研究船舶的運動姿態是非常有利的。
尚無直接預報船舶遭遇角頻率的估計器,研究人員主要通過遭遇角與遭遇角頻率之間的函式關係來間接地計算船舶在當前時刻的遭遇頻率。而該方法存在的主要問題是海浪主浪向的計算較複雜。浪向的獲取主要是藉助於理論或者半經驗海浪波譜、浮標、感測器陣列、波高儀陣列以及雷達衛星等方法。文獻中都是通過船舶的運動獲取海浪方向譜信息。文獻中也僅僅對單自由度二階動力學系統研究船舶航行速度的變化引起遭遇頻率的改變,以此建立了遭遇頻率散射強度與搖盪的關係。以上方法需要的測量設備較多,計算量大。另外,鑒於工程套用的方便和海浪的複雜性,工程人員也常常把長峰波隨機海浪設定為船舶的干擾信號,然而當船舶與海浪之間的遭遇角發生變化時,這種設定不能反應海浪的真實信息,從而會降低船舶的減搖效果。船舶運動信息是由船舶自身的特性和海浪環境的綜合反映,同時也包含了遭遇角頻率信息。基於上述原因,本文通過Welch譜估計方法估計船舶的橫搖角譜,然後計算船舶在最大諧振時的遭遇角頻率。
船舶橫搖數據的獲取
由於測量實船的搖盪信息成本較高,周期較長,為了儘可能的減小船舶航行中信息採集的複雜性和代價,因此,在特定的海況條件下,我們根據平穩線性模型的假設,套用海浪線性疊加理論和MATLAB仿真軟體生成所需要的船舶搖盪信息是一種比較經濟、合理的方法。
譜估計
仿真驗證
在特定海況下進行仿真,即設定海浪有義波高h1/3=3 m,特徵周期T=8 s;船舶的航行速度V=18 kn=9.26 m/s。本文選用中國漁政船32號船的參數,將其代入計算出的船舶橫搖運動的數學模型。由於論文要求的限制,本論文僅以遭遇角μ=90°、150°為例進行了仿真,仿真圖形見圖1至圖2,其中所有(a)圖對應遭遇角μ=90°時的仿真曲線,所有(b)圖對應遭遇角μ=135°時的仿真曲線。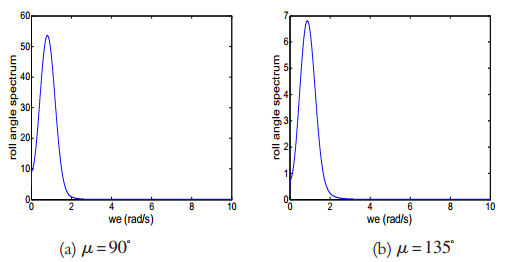 圖2 估算的船舶橫搖角譜
圖2 估算的船舶橫搖角譜
 圖2 估算的船舶橫搖角譜
圖2 估算的船舶橫搖角譜比較可知,遭遇角μ=90°時對船舶的影響比μ=150°時大,通過對圖1和圖2的對比計算,可以得到船舶遭遇角頻率的理論值與估計值的對比表,見表1。
研究結論
首先根據海浪理論和Conolly理論建立了海浪模型和船舶的橫搖模型,然後對 Welch譜估計方法進行了理論推導,最後在特定的海況下進行了仿真驗證。對仿真圖形分析可知:在特定海況、定航速和不同遭遇角下,本文使用的Welch譜估計方法能較好地估算出船舶的遭遇頻率,這為研究海浪與船舶的相互作用提供了有效的方法,為實現船舶減搖的變參數控制提供了可能,但其工程套用價值還有待於實船驗證,本文還需對船舶在不同海況和不同航速下的情形做進一步的研究。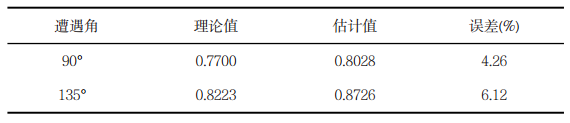 表1 遭遇頻率理論值與估計值的對比表
表1 遭遇頻率理論值與估計值的對比表
 表1 遭遇頻率理論值與估計值的對比表
表1 遭遇頻率理論值與估計值的對比表基於遭遇角決策的並行雙模切換舵減搖控制
為減少風浪條件下艦船橫搖對適航性產生的影響,人們不斷地研究艦船減搖技術。舵減搖是一項新的減搖技術,具有減搖鰭不能替代的優點,如成本低、節省空間、不增加附體阻力、性價比高等,因此有著極其廣闊的套用前景,在世界各國受到極大的關注。
由於橫搖的動態受很多硬的和軟的非線性因素的影響,因此舵減搖控制器的設計往往滿足在某種特定範圍內性能最優以在整個艦船可操範圍內達到次優。文獻採用某些魯棒控制方法以考慮模型不確定性與非線性的影響,如 H∞,LQG與模型預測控制等。這些方法在某些海浪條件下取得的減搖效果一般,尤其是某些尾斜浪(遭遇角在30°~60°範圍)時。究其原因,艦船運動在這些海浪條件下的非線性特性明顯,採用通用線性模型設計的控制器控制性能要下降,而依據模糊線性模型設計的控制器僅僅適用於尾斜浪情況。因此,文中綜合兩種模型的優點,採用一種並行雙模切換控制(parallel two mode switched control,PTMSC)方案,提出一種基於神經網路遭遇角的自動判斷方法,並據判斷結果完成控制器設計模型的決策。
並行雙模轉換控制方案
為驗證控制器性能而進行閉環系統仿真時,應使用非線性艦船模型,以儘可能全面地描述原過程的動態特性。為避免過於複雜的非線性控制器設計過程,在保證和原過程特性大致相同的前提下建立一個較為適宜的線性模型。大多數舵減搖控制器設計主要採用的通用線性模型忽略了所有一階以上或耦合的非線性項,故而此類控制器在艦船處於尾斜浪時的控制效果一般。作者另文簡化出一種模糊線性模型,並基於此模型設計的控制器在尾斜浪情況下控制效果比較好,而在其它情況下可能由於模糊線性化的精度不高,其控制效果並不理想。因此,綜合兩種模型的優點,建立並行雙模切換控制器,使其滿足各種工況條件變化的方案需求。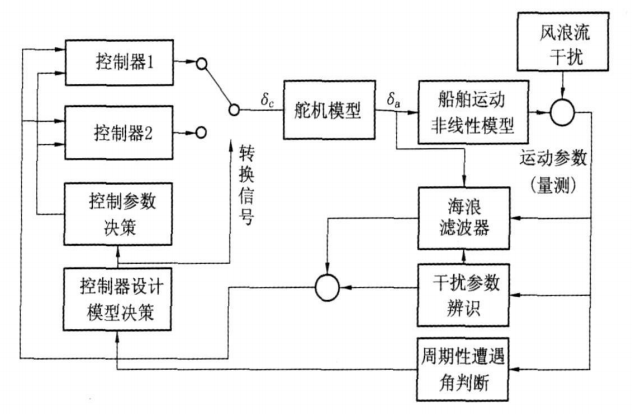 圖3並行雙模切換舵減搖控制結構圖
圖3並行雙模切換舵減搖控制結構圖
 圖3並行雙模切換舵減搖控制結構圖
圖3並行雙模切換舵減搖控制結構圖PTMSC是由許多子系統與控制轉換規則組成的混合系統,其結構如圖3所示。它的控制策略分為高低兩級,高級為根據環境進行的控制器設計模型決策與控制參數決策,低級為兩類控制器。當海況與艦船航行速度相同時,控制器的設計主要依靠遭遇角來決策;當遭遇角相同、海況與航行速度不同時,則主要依靠控制參數來決策,如控制目標中的加權函式。
遭遇角自動判斷
眾所周知,功率譜密度(power spectral density,PSD)是信號的功率在頻域上的分布特性。試驗證明,艦船航行速度與海況相同時,遭遇角不同,艦船橫搖角的功率譜密度就不同。究其原因,遭遇角的改變引起橫搖主導頻率的改變,從而影響橫搖角功率譜密度,因此通過對橫搖PSD的分析來判斷艦船遭遇角就成為可能。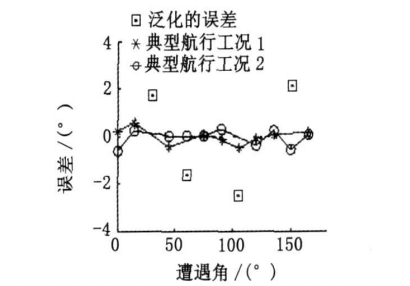 圖4 神經網路訓練與泛化誤差圖
圖4 神經網路訓練與泛化誤差圖
 圖4 神經網路訓練與泛化誤差圖
圖4 神經網路訓練與泛化誤差圖三層神經網路可以實現任意複雜的非線性映射問題。因此,可採用單隱層的三層BP神經網路作為遭遇角自動判斷模型。輸入層為海浪有義波高、平均海浪周期、艦船航速;輸出層為遭遇角。隱層神經元的數目往往與輸入數據中隱含的特徵因素有關,採用試湊法確定。隱層、輸出層的激勵函式均為線性函式。圖4中仿真線型為兩種典型航行工況、不同遭遇角時,採用動量梯度下降算法訓練的單隱層BP神經網路的輸出誤差,方形點為泛化的誤差,誤差均在±3°以內,精度較高。訓練完成後,神經網路固定,則可由現場採集數據,根據神經網路輸出遭遇角供控制器設計模型決策使用。此方法中資料庫數據的所有有用信息均包含於成功訓練好的神經網路中,不必再儲存資料庫數據,節省了存儲空間。且網路固定後,所有權值與闕值均固定,無需線上計算,節省了計算量。由於本方法無CFG法的匹配環節,因此簡化了辨識流程。
研究結論
綜上所述,文中針對單一艦船舵減搖控制方法在艦船航行與海浪處於某些遭遇角時取得的減搖效果一般的問題,採用了並行雙模切換控制方案。為線上自動辨識遭遇角,提出基於橫搖功率譜密度柱狀圖的神經網路辨識方法。仿真結果表明:該方法辨識精度較高,且比傳統重心法節省了線上計算量與需要存儲資料庫的存儲空間,簡化了辨識流程,具有較高的套用價值。
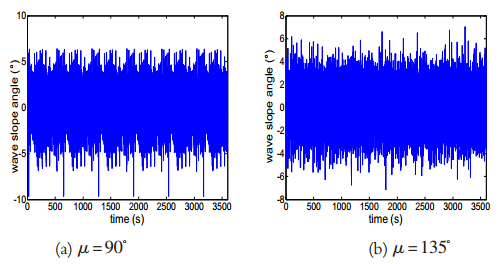 圖1 波傾角
圖1 波傾角