在電力運行、機械加工、大規模的勞動組織等生產過程中,常常會遇到這樣的情況,即不管系統的初始狀態如何,在經歷了一段時問以後,系統就會處於統計平衡狀態(Statistical Equilibrium),這種情況就是數學中所謂的遍歷性問題,遍歷性問題是馬氏鏈理論的一個重要部分。
基本介紹
- 中文名:遍歷性
- 外文名:ergodicity
- 所屬學科:數學
- 屬性:馬氏鏈理論的一個重要部分
定義
遍歷定理
定理1
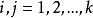
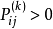

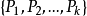
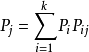
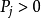

定理2

例題分析

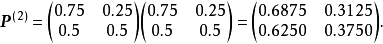
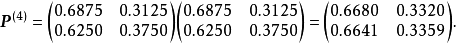
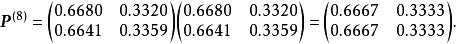
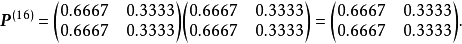

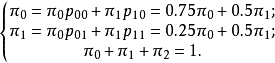
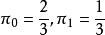
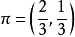


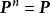
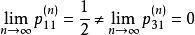

在電力運行、機械加工、大規模的勞動組織等生產過程中,常常會遇到這樣的情況,即不管系統的初始狀態如何,在經歷了一段時問以後,系統就會處於統計平衡狀態(Statistical Equilibrium),這種情況就是數學中所謂的遍歷性問題,遍歷性問題是馬氏鏈理論的一個重要部分。
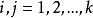
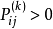

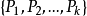
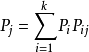
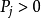



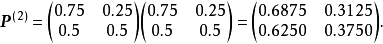
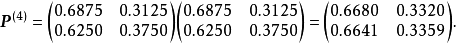
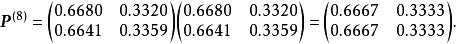
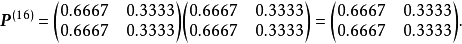

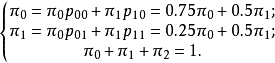
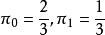
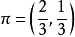


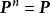
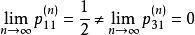
即不管系統的初始狀態如何,在經歷了一段時問以後,系統就會處於統計平衡狀態(Statistical Equilibrium),這種情況就是數學中所謂的遍歷性問題,遍歷性問題是馬氏鏈理論的...
遍歷性理論(ergodic theory)從統計學角度來研究一個系統在長時間內演化性質的一個數學分支.遍歷理論研究的基本課題可參見“動力系統”、“遍歷性”、“保測變換的...
遍歷狀態指的是非周期的正常返狀態。注意這裡的遍歷性指過程無指定間歇地、頻繁地返回,是一個狀態的性質,這與平穩過程的遍歷性是不同的。...
遍歷理論是研究保測變換的漸近性態的數學分支。它起源於為統計力學提供基礎的"遍歷假設"研究,並與動力系統理論、機率論、資訊理論、泛函分析、數論等數學分支有著密切...
平穩隨機過程的遍歷性是在工程技術領域,通過各種技術手段測量得到的數據往往只是隨機過程的一個樣本函式。...
惟一遍歷性(unique ergodicness)遍歷理論研究的一個重要內容.設X為緊緻度量空間,務為其波萊爾6代數,T : X->X為連續映射一}<X,T>表示X上對T不變的波萊爾機率...
各態歷經性又稱遍歷性、埃爾哥得性。隨機過程的一種特性。對於隨機過程似x(t)的樣本函式總體可定義如下的均值ux和自相關函式Rx其中k表示總體中的某一個函式。....
度量可遞性質(保測變換或平穩序列的)(metrically transitive property (of measure-preserving transformation or stationary sequence))是一種與遍歷性有密切關係的...
4.2 dirichlet型的暫留性、常返性、既約性與遍歷性4.3 正則dirichlet型的位勢論第5章 對稱markov過程與dirichlet型5.1 對稱hunt過程與正則dirichlet型i...
