遍歷狀態指的是非周期的正常返狀態。注意這裡的遍歷性指過程無指定間歇地、頻繁地返回,是一個狀態的性質,這與平穩過程的遍歷性是不同的。
基本介紹
- 中文名:遍歷狀態
- 外文名:ergodic state
- 拼音:biàn lì zhuàng tài
- 定義:非周期的正常返狀態
- 相關名詞:周期狀態、遍歷性
- 套用學科:資料庫術語
概述
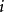

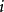
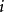
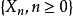
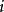

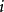
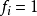
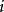
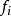
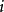
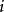
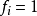
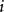
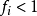
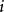
遍歷性
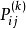
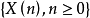
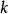

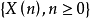
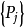
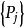
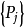
遍歷定理

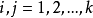
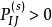
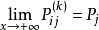
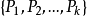
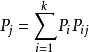
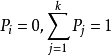
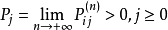
周期狀態和非周期狀態
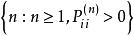
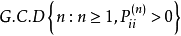
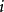
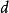
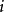
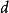
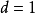
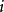
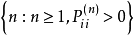
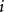
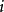
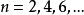

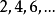
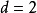
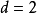
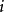
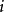
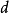
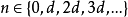
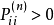

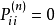


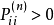
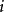

遍歷狀態指的是非周期的正常返狀態。注意這裡的遍歷性指過程無指定間歇地、頻繁地返回,是一個狀態的性質,這與平穩過程的遍歷性是不同的。
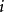

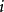
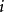
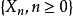
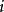

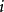
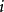
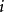
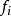
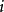
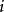
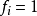
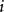
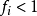
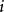
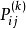
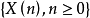
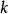
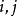
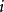

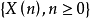
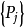
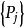
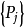

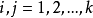
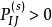
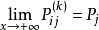
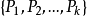
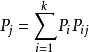
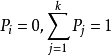
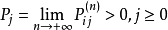
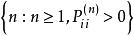
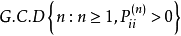
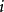
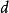
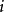
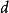
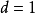
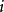
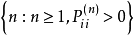
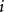
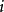
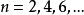

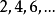
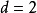
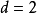
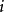
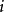
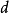
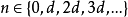
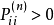

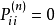


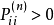
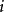
遍歷狀態指的是非周期的正常返狀態。注意這裡的遍歷性指過程無指定間歇地、頻繁地返回,是一個狀態的性質,這與平穩過程的遍歷性是不同的。...
所謂遍歷(Traversal),是指沿著某條搜尋路線,依次對樹(或圖)中每個節點均做一次訪問。訪問結點所做的操作依賴於具體的套用問題, 具體的訪問操作可能是檢查節點的值...
在電力運行、機械加工、大規模的勞動組織等生產過程中,常常會遇到這樣的情況,即不管系統的初始狀態如何,在經歷了一段時問以後,系統就會處於統計平衡狀態(Statistical ...
遍歷理論是研究保測變換的漸近性態的數學分支。它起源於為統計力學提供基礎的"遍歷假設"研究,並與動力系統理論、機率論、資訊理論、泛函分析、數論等數學分支有著密切...
平穩隨機過程的遍歷性是在工程技術領域,通過各種技術手段測量得到的數據往往只是隨機過程的一個樣本函式。...
在G中任選一頂點v為初始出發點(源點),則深度優先遍歷可定義如下:首先訪問出發點v,並將其標記為已訪問過;然後依次從v出發搜尋v的每個鄰接點w。若w未曾訪問過,...
廣度優先遍歷是連通圖的一種遍歷策略。因為它的思想是從一個頂點V0開始,輻射狀地優先遍歷其周圍較廣的區域,故得名。...
《跟超級科學家一起遍歷物質三態》是2011年2月1日龍門書局出版的圖書,作者是比斯庫普。該書是一套兒童書籍,主要通過寓教於樂的方式讓孩子了解物質三態。...
寬度優先遍歷,是以離初狀態的狀態距離為序進行遍歷。...... 寬度優先遍歷,是以離初狀態的狀態距離為序進行遍歷。就是以離初狀態的狀態距離為序進行遍歷。...
3) 對同一個容器對象,可以同時進行多個遍歷。因為遍歷狀態是保存在每一個疊代器對象中的。由此也能得出疊代器模式的適用範圍:1) 訪問一個容器對象的內容而無需...
窮舉測試(exhaustive testing):亦稱完全測試,即程式運行的各個可能分支都應該調試到。窮舉法,可視為最簡單的搜尋。即是在一個可能存在可行狀態的狀態全集中依次遍歷...
