運輸問題

運輸問題，一類具有特殊結構的線性規劃問題。由於運輸問題約束方程組的係數矩陣是完全么模的，即所有的子行列式為0或±1，存在著比單純形法更簡單的特殊解法。

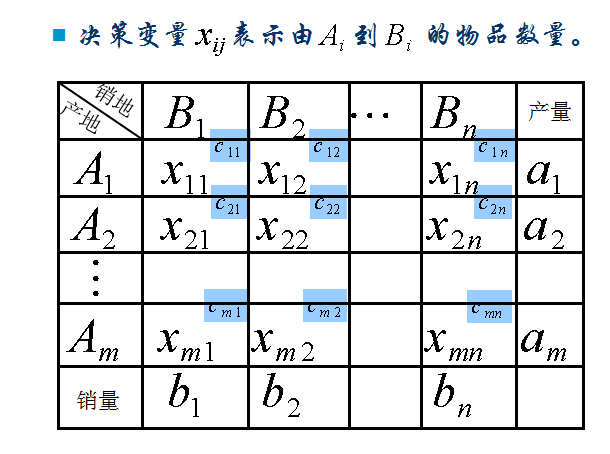
基本介紹

• 中文名：運輸問題
• 外文名：Transportation problem
• 別名：運輸型問題
• 學科歸屬：交通科學、運籌學

問題類型

現已發現的運輸型問題有以下6類：

1. 一般運輸問題，又稱希契科克運輸問題，簡稱H問題。
   
2. 網路運輸問題，又稱圖上運輸問題，簡稱T問題。
   
3. 最大流量問題,簡稱F問題。
   
4. 最短路徑問題，簡稱S問題。
   
5. 任務分配問題，又稱指派問題,簡稱A問題。
   
6. 生產計畫問題，又稱日程計畫問題，簡稱CPS問題。
   

如把產地稱為源（發點），銷地稱為匯(收點)，則任務分配問題、生產計畫問題等運輸型問題的模型也可以歸納成類似上述形式。本詞條的運輸問題指的是一般類型的運輸問題。

運輸模型

問題提出

圖1.問題舉例

運輸問題的典型情況是研究單一品種物質的運輸調度問題：設某種物品有m個產地A₁，A₂，···，A_m，各產地的產量分別是a₁，a₂，···，a_m；有n個銷地B₁，B₂，···，B_n，各個銷地的銷量分別為b₁，b₂，···，b_n。假定從產地Ai(i=1,2,···,m)向銷地Bj(j=1,2,···,n)運輸單位物品的運價為c_ij，問怎么調運這些物品才能使總運費最小？

數學模型

產銷平衡運輸問題的數學模型可表示如下：

式中min表示求極小值，因為目標函式表示運輸總費用，要求其極小化，S.T.表示“約束條件為”。約束條件中前m行的意義是由某一個產地A_i運往各個銷地的物品數量x_ij之和等於該產地的產量a_i，後n行的意義是由某一個產地B_j運往各個銷地的物品數量x_ij之和等於該銷地的銷量b_i，最後一行表示變數非負約束，因為物品為負數無意義。

如果運輸問題的總產量等於總銷量，即有當ɑi，bj滿足此條件時稱為產銷平衡的運輸問題，否則稱為產銷不平衡的運輸問題。產銷不平衡的運輸問題可以通過增加假想產地或假想銷地，化成產銷平衡的運輸問題。

以上模型是一種線性規劃模型，單純形法師求解線性規劃問題十分有效的一般方法，因而單純形法也可以求解運輸問題。但是採用線性規劃的單純形法求解運輸問題時，先得在每個約束條件中引入一個人工變數，即使求解3個產地，4個銷地(m=3,n=4)這樣的簡單運輸問題，在不考慮去掉多餘約束條件的情況下，變數數目也會達到19個之多，因而需要尋求更簡便的解法。

係數矩陣

將約束條件的結構加以整理，可知運輸模型約束方程組的係數矩陣具有下述比較鬆散且特殊的形式：

圖2.運輸模型約束方程組的係數矩陣

其係數列向量的結構式：A_ij=(0,···,0,1（第i個）,0,···,0,1（第m+j個）,0,···,0)^T，即除第i個和第(m+j)個分量為1外，其他分量全等於0。這是(m+n)×mn的矩陣，每一列的元素中只有2個1，其餘均為0。可以證明A的秩=(m+n－1)，所以運輸問題的任一基本可行解都有(m+n-1)個基變數，這(m+n-1)個基變數的值就對應一個調運方案。

由此可知，運輸問題的約束條件具有下述特點：

1. 運輸問題的有m×n個變數，(m+n)個約束方程，(m+n-1)個基變數。
   
2. 約束條件係數矩陣的元素等於0或1。
   
3. 約束條件係數矩陣的每一列有兩個非零元素，這對應於每一個變數在前m個約束方程出現一次，在後n個方程中也出現一次。
   

對產銷平衡運輸問題，除上述兩個特點外，還有以下特點：

1. 所有結構約束條件都是等式約束。
   
2. 各產地產量之和等於各銷地銷量之和。
   

有限最優解

對產銷平衡的運輸問題，可以找到一個可行解：其變數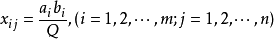 是運輸問題的一個可行解，其中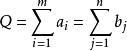， ，目標函式有下界0，目標函式值不會趨於 。由此可知，運輸問題必存在有限最優解。

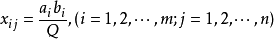
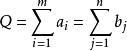
運輸表

這是有多個產地供應多個銷地的單一品種物資運輸問題。為直觀清楚起見，可列出該問題的運輸表，如下表所示。

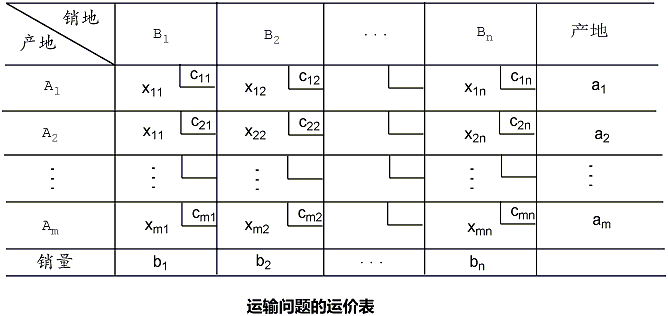圖3.運輸表

表中的變數x_ij(i=1,2,···,m;j=1,2,···,m)為產地A_i運往銷地B_j的物品數量，c_ij為A_i到B_j的單位運價。有時，僅簡單地將單位運價單獨列入另一個表中，稱其為運價表，如下表所示。

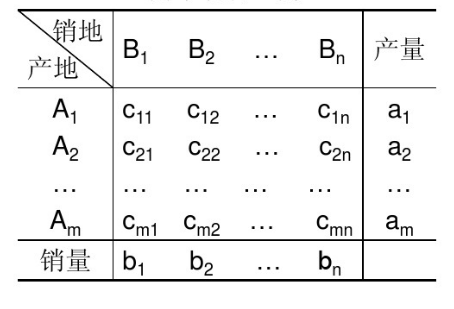圖4.運價表

求解方法

求解思路

根據運輸問題的數學模型求出的運輸問題的解X=(x_ij)，代表著一個運輸方案，其中每一個變數x_ij的值表示由A_i調運數量為x_ij的物品給B_j。前已指出運輸問題是一種線性規劃問題，可構想用疊代法進行求解，即先找出它的某一個基可行解，在進行解的最優性檢驗，若它不是最優解，就進行疊代調整，以得到一個新的更好的解，繼續檢驗和調整改進，直到得到最優解為止。

為了能按照上述思路求解運輸問題，要求每步得到的解X=(x_ij)都必須是其基可行解，這意味著：

1. 解X必須滿足模型中的所有約束條件；
   
2. 基變數對應的約束方程組的係數列向量線性無關；
   
3. 解中非基變數的個數不能大於(m+n-1)個，原因是運輸問題雖有(m+n)個結構約束條件，但是由於總產量等於總銷量，故只有(m+n-1)個結構約束條件是線性獨立的；
   
4. 為使疊代順利進行，基變數的個數在疊代過程中應該始終保持為(m+n-1)個。因為可以證明(m+n-1)基變數所對應的約束方程的係數列向量線性無關。
   

表上作業法

當採用一般單純形法求解運輸問題時，應去掉一個多餘的約束等式，任何一個約束等式均可。但運輸問題是的特殊性，人們將單純性法簡化用表格來處理，採用表上作業法求解時，因為在運輸表上進行，不必寫出上述的數學模型。

運輸問題解的每一個分量，都唯一對應其運輸表中的一個格。得出運輸問題的一個基可行解後，就將即便基變數的值x_ij填入運輸表相應的格子(A_i,B_j)內，並將這種格子稱為填有數字的格，含填數字0的格，這時的解為退化解，退化需要補0；對非基變數對應的格不填入數字，稱為空格。

表上作業法是求解運輸問題的一種簡便而有效的方法，其求解工作在運輸表上進行，它是一種疊代法，可以滿足上述的要求，疊代步驟為：先按照某種規則找出一個初始調運方案；再對現行解做最優性判別；若這個解不是最優解，就在運輸表上對它進行調整改進，得出一個新的解；再判別，再改進；直到得到運輸問題的最優解為止。

初始基本可行解

表上作業法的第一步就是找出一個初始解，初始基本可行解的求法介紹三種。

左上角法

西北角法，它的基本思想是給運輸表中左上角的變數分配運輸量以確定產銷關係。

最小元素法

最小元素法，或最小成本法。它的基本思想是就近供應，即從運輸表中運價最小的格子開始分配運輸量以確定產銷關係。

元素差額法

又稱沃格爾近似法，簡稱VAM法。它是從運輸表中各行和各列的最小元素和次小元素的差額來確定產銷關係。

最優性檢驗

得到了運輸問題的初始基可行解之後，即對應這個解進行最優性判別，看它是不是最優解。改進初始基本可行解有兩種最常用的方法：閉迴路法和對偶變數法（位勢法）。

閉迴路法

這種方法需要對每一個空格尋找一條閉迴路，並根據閉迴路求出每個空格的檢驗數。當運輸問題中m和n較大時，計算檢驗數的工作量很大。

位勢法

或乘數法。先對初始調運方案求出位勢，然後求各空格的檢驗數。當所有的檢驗數均為非負時，就得到最優方案。如果出現負的檢驗數，則從檢驗數為負的空格出發，作閉迴路，重新計算檢驗數，作進一步調整。用位勢法求檢驗數就是對偶問題的表上作業法。