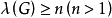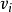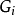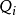連通圖G的連通程度通常叫做連通度(Connectivity)。連通度有兩種,一種是點連通度,另一種是邊連通度。通常一個圖的連通度越好,它所代表的網路越穩定。
基本介紹
- 中文名:連通度
- 外文名:connectivity
- 所屬學科:數學
- 分類:點連通度、邊連通度
- 意義:代表網路穩定程度
基本概念,知識儲備,定義,相關定理,定理1,定理2,定理3,
基本概念
知識儲備
如果在圖G中刪去一個結點x後,圖G的連通分支數增加,即 ,則稱結點x為G的割點(cut vertex)。如果在圖G中刪去一條邊e後,圖G的連通分支數增加,即
,則稱結點x為G的割點(cut vertex)。如果在圖G中刪去一條邊e後,圖G的連通分支數增加,即 ,則稱e為G的割邊(cut edge)或橋。
,則稱e為G的割邊(cut edge)或橋。


沒有割點的非平凡連通圖稱為塊( block)。G中不含割點的極大連通子圖稱為圖G的塊。
若H是圖G的塊,則H自身不含割點且滿足:若向H中再添加邊,但不添加結點,那么H就不是G的子圖了;若向H中再增加結點或邊將H擴大為更大的連通圖,那么H就會含有割點。
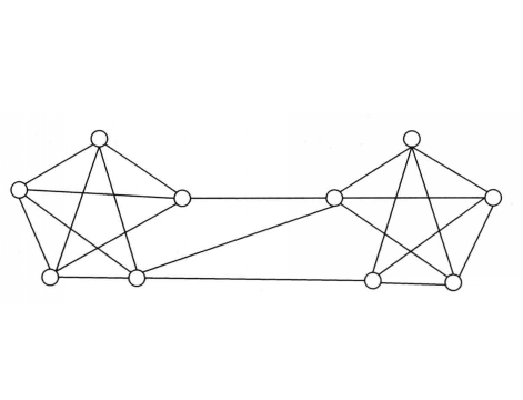
例如,圖1所示圖G的塊如圖2所示。
 圖1
圖1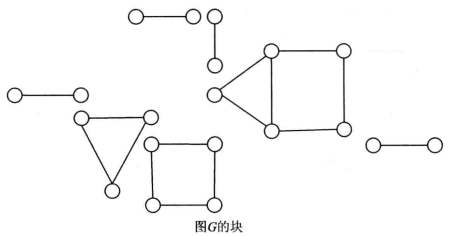 圖2
圖2如果圖G的頂點集的一個真子集T滿足G-T不連通或是平凡圖,則稱T為G的一個點割( vertex cut)。如果圖G的邊集的一個真子集S滿足G-S不連通或是平凡圖,則稱S為G的一個邊割(edge cut)。
定義
設G是連通圖,稱 為G的點連通度( vertex connectivity)或連通度;稱
為G的點連通度( vertex connectivity)或連通度;稱 為G的邊連通度(edge conncctivity)。
為G的邊連通度(edge conncctivity)。


相關定理
定理1
對一個圖G,有 。其中
。其中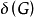 是圖G的最小頂點度。
是圖G的最小頂點度。

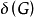
證明 若G不連通,則 .故上式成立。若G連通,則:
.故上式成立。若G連通,則:

(1)先證 。
。

設x是G中度數最小的頂點,即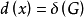 ,設所有與x關聯的邊集為S (x),顯然x是圖G-S(x)的一個孤立結點。於是
,設所有與x關聯的邊集為S (x),顯然x是圖G-S(x)的一個孤立結點。於是 。
。
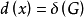

(2)再證 。
。

當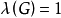 時,顯然有
時,顯然有 。
。
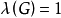

假設對所有 的圖G,有
的圖G,有 。再設
。再設 ,S是H的一個邊割,且
,S是H的一個邊割,且 。若邊
。若邊 ,易知
,易知 ,故由假設知
,故由假設知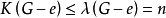 ,並設T是
,並設T是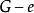 的一個點割,且
的一個點割,且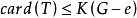 。而此時
。而此時 就是H的一個點割,即
就是H的一個點割,即






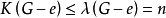
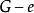
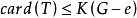


由歸納法原理知 。證畢。
。證畢。

定理2
設圖G是n連通的,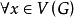 ,則
,則 。
。
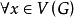

證明 假設G有一個頂點y且 ,即y與n一1條邊關聯。設與y關聯的n一1個頂點構成的集合為S,顯然S是G的一個點割。因而
,即y與n一1條邊關聯。設與y關聯的n一1個頂點構成的集合為S,顯然S是G的一個點割。因而 。這與
。這與 矛盾。
矛盾。



定理3
若G是2邊連通圖,則G有強連通的定向圖。