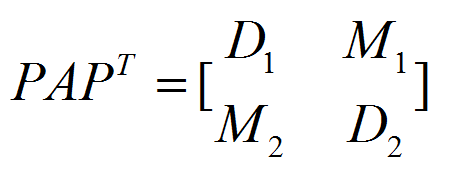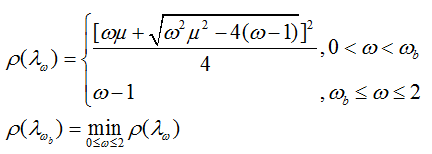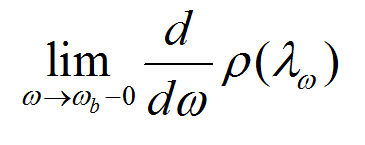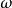逐次超松馳疊代法

D. M. Young於20世紀70年代提出逐次超鬆弛(Successive Over Relaxation)疊代法，簡稱SOR方法，是一種經典的疊代算法。它是為了解決大規模系統的線性等式提出來的，在GS法基礎上為提高收斂速度，採用加權平均而得到的新算法。由於超鬆弛疊代法公式簡單，編製程序容易，很多工程學、計算數學中都會套用超鬆弛疊代方法。使用超鬆弛疊代法的關鍵在於選取合適的鬆弛因子，如果鬆弛因子選取合適，則會大大縮短計算時間。

基本介紹

• 中文名：逐次超鬆弛疊代法
• 外文名：successive over relaxation iteration method
• 簡稱：SOR法
• 提出時間：20世紀70年代
• 提出者：D. M. Young
• 關鍵技術：鬆弛因子值的選取

簡介

為解決實際問題中大維數線性代數方程組的求解問題，提出了許多疊代法。但大多數疊代法不是對各類線性方程組都有收斂性。在解題時，對原方程組矩陣作一根本的變換，從而可能使條件數變壞，也可能破壞了變換前後方程組的等價性，以及喪失使原方程組的對稱性等。通過對GS法進行改進，從而產生了逐次超鬆弛(SOR)疊代法。

SOR方法的思路為：如果能夠簡單有效地確定單個樣本加入樣本集後對訓練結果的影響，一方面，出現新的樣本時可以利用原來的一訓練結果而不必重新開始；另一方面，讓訓練樣本逐個進入樣本集可以簡化尋優過程，提高算法速度。這實際上是將樣本集中的樣本數減少到一個。

對於逐次超鬆弛疊代法，鬆弛因子的選取對算法的收斂速度有很大影響，通常對於方程組Ax=Y，若A為正定矩陣，則當0< <2時，逐次超鬆弛疊代恆收斂。

逐次超鬆弛疊代法與Jacobi疊代法、Seidel疊代法等相比收斂速度較快。由逐次超鬆弛疊代法求出的方程組的數值解具有較高的精確性。逐次超鬆弛疊代法可以大大減少計算量和計算機的記憶體儲量，從而提高計算效率。逐次超鬆弛疊代法可以廣泛地套用於實際，如支持向量機算法中求最大分類間隔的二次規劃問題、解高階稀疏線性方程組等。

逐次超鬆弛疊代法的定義

設已求得n元線性代數方程組Ax=b第k -1次疊代向量 及第k次疊代向量 的分量 ，要計算分量 。

(1) 用Gauss-Seidel(GS)疊代求得： ；

(2) 計算 與第k -1次疊代值 的加權平均 作為第k次疊代值：

或整理成： ， 。

其中，參數 稱為鬆弛因子，0< <2。當 >1時，上式稱為逐次超鬆弛疊代法；當 =1時，上式為Gauss-Seidel疊代法；當0< <1時，上式稱為低鬆弛疊代法。

逐次超鬆弛疊代法的收斂性判別

收斂性判別條件

SOR疊代法收斂的充分必要條件是ρ(λω)<1，ρ(λω)與鬆弛因子ω有關。ρ(λω)與ω的關係以及SOR方法收斂的條件有如下定理。

定理1：(Kahan)對任意的A ，設其對角元皆非零，則對所有實數ω，有：ρ(λω)≥ ω-1。

推論：如果解Ax=b的SOR方法收斂，則有ω-1<1，即0<ω<2。

定理2：(Ostrowski-Reich)設A ，A對稱正定，且0<ω<2，則解Ax=b的SOR方法收斂。

收斂速度的估計

SOR疊代法的疊代矩陣λω與ω有關，當選取不同的ω時，其疊代速度也有所不同。因此，需要找到最優的鬆弛因子 ，使對應 的SOR方法收斂最快。

定理3　設A ，A=D-L-U為LU分解。如果存在排列矩陣P，使：

其中， 、 為對角方陣，則稱A是2-循環的。此外，若當 ≠0時，矩陣 的特徵值都和 無關，則稱A是相容次序矩陣。

定理4：設A ，A有非零的對角元，且是2-循環和相容次序的；又設 是方程組Ax=b的Jacobi疊代的疊代矩陣，且 的所有特徵值均在[0,1)上。記μ=ρ(B)及 。則方程組的SOR方法疊代矩陣的譜半徑ρ(λω)滿足：

且當0<ω< 時，ρ(λω)是ω的單調減函式，並有

逐次超鬆弛疊代法鬆弛因子的選取

SOR疊代方法中鬆弛因子的取值直接影響到算法的收斂性及收斂速度。若選擇得當，可以加快收斂速度，甚至可以使發散的疊代變成收斂。因此，鬆弛因子取值的選取是SOR方法能否成功的關鍵。為了保證疊代過程的收斂，必須要求o< <2，對超鬆弛法去1< <2。只有在係數矩陣具有少數特殊類型的情況下，才能通過數學公式確定鬆弛因子。對於一般情況，有如下取值方法。

二分比較法

將鬆弛因子 的區間(1，2)進行二分，每個小區間的長度為1/2， 取區間中點值3/2，按照SOR疊代公式疊代，求出疊代次數k。如果k不超過指定的發散常數，則可確定 的值；否則將(1，2)區間四等分，每個小區間的長度為1/4， 取各分點的值，繼續疊代。一般地，將區間(1，2)二分M次，每次二分步長為 ， 依次取各二分點的值，按照SOR疊代公式疊代，並求出疊代次數k值。如果k值不超過指定的發散常數，則可確定 的值，這樣總能找到一個不超過指定發散常數的 值。算法描述如下：

(1) 給定發散常數RADIATl0N的值，令二分次數M的初始值為1；

(2)將區間(1，2)二分M次，每次二分的步長為 ， 取各二分點的值；

(3) 對每一個二分點SOR疊代公式疊代求出疊代次數k；

(4) 比較各二分點的k值找出最少疊代次數的 值；

(5) 判斷若 小於RADIATl0N，則結束；否則二分次數M++，轉步驟(2)繼續二分。

逐步搜尋法

將 的取值區間(1，2)進行M等分， 分別取 。通過SOR疊代公式依次對同一個精度要求求出疊代次數k的值，並從中選出最優鬆弛因子 的值。算法描述如下：

(1) 給定等分數M和精度要求的值，令的初始值為1；

(2) 令p=1，2，…，M一1，重複步驟(3)-(5)；

(3) ；

(4) 按照如下公式疊代：

其中，。找出符合精度要求的疊代次數；

(5)比較找出使值最小的，即為最優鬆弛因子的值。

黃金分割法

依據黃金分割法的思想，通過計算機自動選取最優鬆弛因子的近似值，算法描述如下：

(1) 對(1，2)區間第一次0.618的分割，區間邊界a1=1，b1=2，在(a1，b1)區間分割出黃金t1=a1+0.618(b1-a1)，進行SOR法的疊代，求出疊代次數k值。如果疊代次數沒有超出規定的發散常數，疊代結束；否則轉步驟(2)。

(2) 在(1，1.618)和(1.618，2)之間進行第二次的黃金分割，找出分割點t2=a2+0.618(b2-a2)，其中a2和b2是新分割區間的左右邊界。找出疊代次數最少的。發散則改變區間繼續進行黃金分割。

MATLAB實例程式（解線性方程組）

%---逐次超鬆弛疊代法-----
%---successive over-reaxation iteration method
clear;clc;
A=[10,-1,-2;-1,10,-2;-1,-1,5];
b=[72,83,42]';
N=length(b); %解向量的維數
fprintf('庫函式計算結果：');
x=inv(A)*b %庫函式計算結果

x=zeros(N,1);%疊代初始值
%-----(A=D-E-F)------
D=diag(diag(A));
E=-tril(A,-1);%下三角
F=-triu(A,1);%上三角
w=1.1; %鬆弛因子，一般0<w<2
B=inv(D-w*E)*[(1-w)*D+w*F];g=w*inv(D-w*E)*b;
eps=0.00001;%相鄰解的距離小於該數時，結束疊代

%--------開始疊代-------
for k=1:100 %最大疊代次數為100
fprintf('第%d次疊代：',k);
y=B*x+g;
if abs(x-y)<eps
break;
end
x=y
end
x