基本介紹
- 中文名:逆變換採樣
- 外文名:inverse transform sampling
簡介
定義
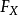
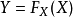
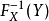
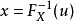
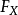
示例
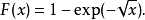
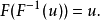
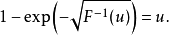
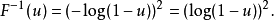
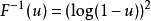
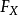
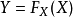
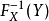
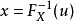
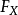
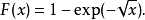
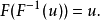
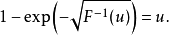
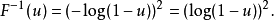
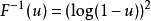
逆變換採樣(英語:inverse transform sampling),又稱為逆採樣(inversion sampling)、逆機率積分變換(inverse probability integral transform)、逆變換法(inverse ...
這裡的反變換即逆Z變換,是由信號序列的Z變換反回去求原信號序列的變換方式。...它後來於1952年在哥倫比亞大學被Ragazzini和Zadeh冠以“the z-transform“用於採樣...
②式的積分運算叫做F(ω)的傅立葉逆變換。F(ω)叫做f(t)的像函式,f(t)叫做 F(ω)的像原函式。F(ω)是f(t)的像。f(t)是F(ω)原像。 ①傅立葉...
全書分三部分,首先闡述線性代數、傅立葉分析和結合採樣計算的各種代表性信號;其次,其基礎理論內容涵蓋子空間和光滑先驗的採樣,包括非線性採樣和採樣率變換等基礎知識...
離散時間傅立葉變換(英語:Discrete-time Fourier Transform,簡稱:DTFT)是傅立葉變換的一種。它將以離散時間nT(其中,T為採樣間隔)作為變數的函式(離散時間信號)...
計算逆變換(j1,i1)和(j1,i1);逐行掃描目標圖像g(x1,y1),對於g(x1,y1)...插值法是一種最簡單的插值算法,輸出像素的值為輸入圖像中與其最鄰近的採樣點的...
2.8.3Z變換與傅立葉變換的關係 2.8.4Z變換的性質 2.8.5Z逆變換 2.8.6用Z...3.3.4採樣定理及離散沃爾什變換 3.3.5離散沃爾什變換的性質 3.3.6沃爾什變換...
改進離散餘弦變換(Modified Discrete Cosine Transform ),簡稱MDCT,是一種線性正交...36個採樣點為例,如圖1(a),利用MATILAB可以得到信號經過MDCT及其逆變換後的波形...
//快速傅立葉變換 // 入口參數: // l: l=0, 傅立葉變換;l=1, 逆傅...// pr[]: l=0時,存放N點採樣數據的實部 // l=1時, 存放傅立葉變換的...
其中T是用在推導雙線性變換的梯形公式中數值積分每階的大小,換句話說就是採樣...逆映射則為雙線性變換的本質是使用這種一階估計法且將連續時間傳遞函式 中的s...
《快速傅立葉變換:算法與套用》是2013年出版的一本圖書,作者是K.R.Rao。...7?3?2NDFT的逆變換(INDFT)1847?4二維NDFT1887?4?1二維採樣結構188...
均勻分布對於任意分布的採樣是有用的。 一般的方法是使用目標隨機變數的累積分布函式(CDF)的逆變換採樣方法。 這種方法在理論工作中非常有用。 由於使用這種方法的...
這些條件具有定義傅立葉變換的積分及其逆的絕對可積分的優點。這個條件是上面在...DFT是連續傅立葉變換的近似。因此可以對連續信號x(t)均勻採樣並截斷以得到有限...
模數變換主要是對模擬信號進行採樣,然後量化編碼為二進制數位訊號;數模變換是模數變換的逆過程,主要是將當前數位訊號重建為模擬信號。下面主要介紹採樣和重建的方法。...
數模轉換就是將離散的數字量轉換為連線變化的模擬量。與數模轉換相對應的就是模數轉換,模數轉換是數模轉換的逆過程。接下來我們將從轉換器的分類,技術指標,模數變換...
,臨界採樣的因子Ω是類似於DFT(離散傅立葉變換),獲得分成N個離散分區的頻域。然後,這N個頻譜分區的逆變換導致時間窗的N值y(k),其由N個樣本值組成。對於具有N...
5.2.1逆系統設計5.2.2數字濾波器設計5.3全通系統和最小相位系統 [2] 5....7.6.3希爾伯特變換器設計7.7本章小結習題第8章多採樣率信號處理...
