迴避交叉（avoided crossing）是2019年發布的物理學名詞。
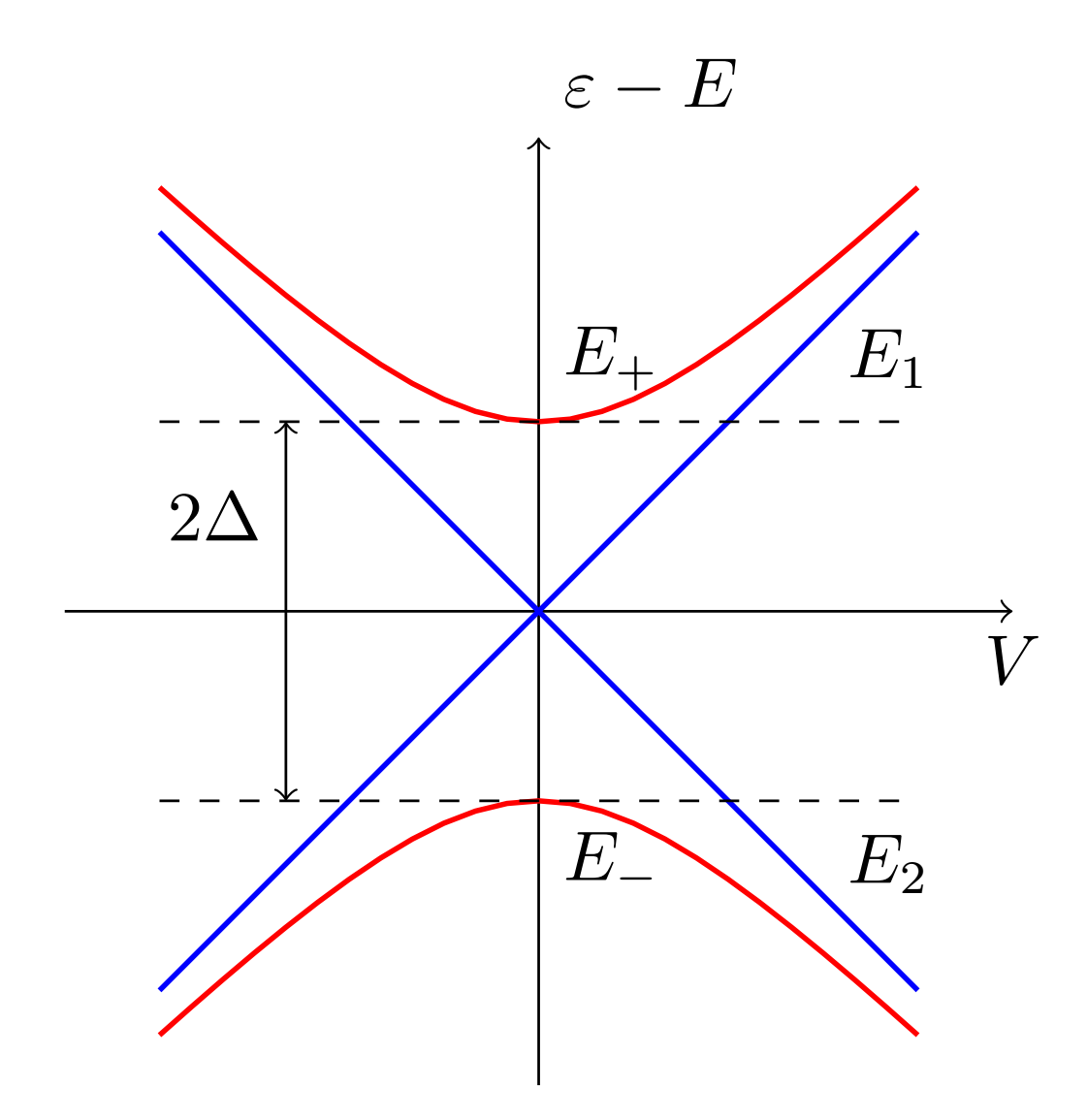
在量子物理和量子化學中，所謂的能級迴避交叉（level avoided crossing），或者說能級排斥（level repulsion）現象指的是：用來表示某個量子可觀測量且依賴於 N 個連續實參量的厄米矩陣所具有的兩個本徵值無法相等（即“交叉（corss）”），除非是在 (N − 2) 維的流形上。這種現象也被稱為馮·諾伊曼-維格納定理（von Neumann–Wigner theorem）。在雙原子分子的情形下（只有一個參量，即鍵長），這意味著本徵值根本不能交叉。在三原子分子的情形下，這意味著本徵值只能在某一點處相等（參見圓錐交叉（conical intersection））。
這在量子化學中尤為重要。在玻恩-奧本海默近似（Born–Oppenheimer approximation，簡稱 BO近似）中，分子的電子哈密頓量被對角化在一組不同的分子幾何圖形上（得到的本徵值即為絕熱勢能面的值），而勢能面迴避交叉後的幾何圖形便是玻恩-奧本海默近似失效後的軌跡。
基本介紹
公布時間,出處,在二態系統中的湧現,
公布時間
2019年經全國科學技術名詞審定委員會審定發布。
出處
《物理學名詞》第三版。
在二態系統中的湧現
二能級系統（two-level system）的研究在量子力學中具有重要意義，因為它可以簡化許多物理系統。畫出個體能量關於能量差的本徵態曲線，通過觀察曲線中的迴避交叉，可以看出微擾對二態系統哈密頓量的影響。二態哈密頓量可寫成
其本徵值為
和
，本徵矢量為
和
。這兩個本徵矢量對應於系統的兩種狀態。如果系統一開始處於其中一種狀態下，那么它將保持在該狀態。當恰好等於時，哈密頓量將出現二重簡併。顯然，在這種情形下，簡併本徵態的任意疊加態都是哈密頓量的另一個本徵態。因此，在任意狀態下開始的系統都將永遠保持在原來的狀態。
然而，當受到外部微擾時，哈密頓量的矩陣元發生了變化。為了簡單起見，我們考慮一個只有非對角元素的微擾。由於總的哈密頓量必須是厄米的，所以我們可以把新的哈密頓量簡單寫成
其中，
是對角項為零的微擾。因為是厄米矩陣，所以它的非對角分量固定。修改後的本徵態可通過對修改後的哈密頓量進行對角化得到。結果，新的本徵值為
如果沿著橫軸繪製
，沿著豎軸繪製
或
，我們可以看到雙曲線的兩個分支。曲線漸近地接近原始的非微擾能級。分析曲線可以看出，即使原始的態是簡併的（即
），新的態也不再相等。然而，如果設 ∆ 為 0，我們便會發現在
處，
且能級交叉。因此，由於微擾的影響，這些能級交叉被迴避了。
能級迴避交叉示意圖。
