基本介紹
- 中文名:近似平差
- 外文名:Approximate adjustment
- 描述:近似坐標測量方法
- 套用:附合導線
- 學科:數學
概念
卡西歐fx-4800P計算器附合導線近似平差程式
研究背景
附合導線近似平差程式
 圖1 附合導線
圖1 附合導線研究結論
附合導線測量近似平差方法及點位精度分析
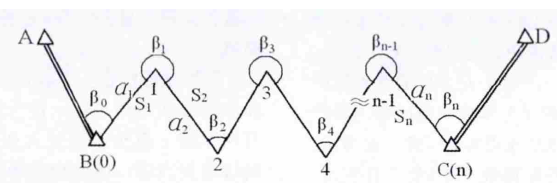 圖2 附合導線示意圖
圖2 附合導線示意圖測量原理與方法
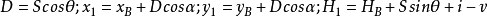
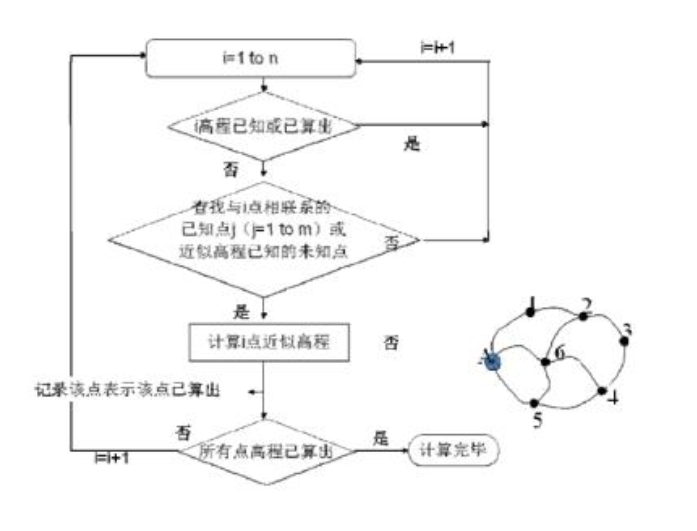
 圖1 附合導線
圖1 附合導線 圖2 附合導線示意圖
圖2 附合導線示意圖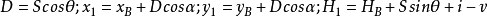
近似平差配合全站儀不僅可以直接測量距離和角度,也可以直接進行坐標測量,給測量工作帶來極大方便。套用全站儀附合導線坐標測量的近似平差計算方法,並對點位的精度進行...
序慣平差也叫逐次相關間接平差,它是將觀測值分成兩組或多組,按組的順序分別做相關間接平差,從而使其達到與兩期網一起做整體平差同樣的結果。...
四、中點多邊形近似平差第五節解析交會測量一、概述二、前方交會三、側方交會四、後方交會第六節輻射點的計算思考題與習題第八章高程控制測量...
多餘觀測是測量平差計算中的一個術語。它是指在一組觀測值中,除了能惟一確定某個幾何或物理模型的t個必要觀測之外的其餘觀測值。多餘觀測即觀測值的個數多於確定...
現以兩端有基線的小三角鎖為例,闡述近似平差的計算方法。圖為兩端有基線的小三角鎖,A、B為高級控制點,EF為實測基線邊,設AB為do、EF為dn,方位角αAB為已知,...
7 4 4中心多邊形近似平差計算225 7 4 5前方交會法227 7 5建築方格網229 7 5 1方格網的基本要求230 7 5 2建築方格網的設計231 7 5 3建築方格網的測設...
獨立模型法空中三角測量,是指以單模型、雙模型或幾個模型組成的單元模型為整體平差運算中的基本單元的區域網空中三角測量。...
是一種用於公路、鐵路、城市道路主線、立交匝道的勘測設計與施工放樣工作的軟體。包括導線測量平差、道路全線測設、 橫斷面及工程量、局部曲線測設、常用測量計算工具...
7.4.4中心多邊形近似平差計算226 7.4.5前方交會法228 7.5建築方格網230 7.5.1建築方格網的基本要求230 7.5.2建築方格網的設計232 7.5.3建築方格網的測設232...
第一節 施工導線近似平差公式第二節 施工導線近似平差公式程式編寫一、附合導線觀測角平差程式編寫二、閉合導線觀測角平差程式清單...
2.1導線的近似平差計算程式2.2跨牆圖根導線的平差計算程式2.3無定嚮導線的計算程式2.4圖根支導線的計算程式2.5測邊交會點的坐標計算程式...
第七節 三維坐標附合、閉合導線近似平差計算程式第八節 水準路線平差計算程式第九節 橋樑三角網近似平差計算程式第十節 隧道三角鎖近似平差計算程式...
二、以坐標和高程為觀測值的導線近似平差計算241第五節GPS平面控制測量244一、GPS控制網的分級244二、GPS點的密度245三、測量作業基本技術規定246...
1.8 複數形式任意單一導線近似平差原理與程式(qh1-8t) 1.9 程式語句與常用提示字元的輸入方法 2含斷鏈的交點法任意路線或匝道曲線三維坐標計算程式 2.1 單交...
四、中點多邊形近似平差第五節 解析交會測量一、概述二、前方交會三、側方交會四、後方交會第六節 輻射點的計算思考題與習題第八章 高程控制測量...
1.8 複數形式單一閉、附合與無定嚮導線近似平差原理與程式(QH1-8)1.9 複數形式支導線坐標計算程式(QH1-9)2 公路與鐵路路線平縱曲線正、反算原理與程式...
第九節 三維坐標附合、閉合導線近似平差計算程式第十節 橋樑三角網平差計算程式第十一節 隧道三角鎖平差計算程式第十二節 隧道測量坐標與施工坐標換算程式...
(Q4V2) 2.3 單一閉附合等級導線條件平差程式(Q4V3/H4V3) 2.4 水準網間接平差程式(Q4V4/H4V4) 2.5 複數形式任意單一導線近似平差程式(Q4V5) 練習題第...
第三節導線平差計算程式 一、導線近似平差分步計算程式 二、單一導線嚴密平差計算程式 三、複測支導線計算程式 四、支導線坐標計算程式(引點坐標計算程式)...
(Q4V2) 4.3 單一閉附合等級導線條件平差程式(Q4V3/H4V3) 4.4 水準網間接平差程式(Q4V4/H4V4) 4.5 複數形式單一閉附合與無定嚮導線近似平差原理與程式(...
2.5 複數形式任意單一導線近似平差程式(Q4V5) 練習題 [2] 第3章 水準測量記錄程式3.1 一、二等水準測量記錄程式(Q3V1/H3V1)...
