近乎處處

簡介

在測度論（數學分析的一個分支）中，在某種意義上，如果集合的屬性幾乎包含了所有可能性，那么這個屬性是近乎處處的。近乎處處的概念是測度零概念的同伴概念。在機率主體中，這主要是基於測度理論，並且這個概念幾乎可以肯定地被認為。

更具體地說，如果元素集合的屬性沒有不成立的就是測度零的集合（Halmos 1974）。在討論實數集時，除非另有說明，否則將採用勒貝格度量。

這個術語近乎處處可以縮寫為a.e。在較早的文獻中被用來代替等效的法語預言片。

一個完整測度的集合的補碼是測度零集。在機率理論中，這些術語幾乎可以肯定地，幾乎是確定的，幾乎總是指機率為1的事件，它們是機率空間中完全度量的集合。

有時候，不用說一個屬性近乎處處，而是說成這個屬性幾乎適用於所有元素（雖然這個術語幾乎都有其他含義）。

如果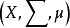

是測度空間，則如果μ（{x∈X：¬P(x)}）= 0，那么P就被說成是近乎處處的。表達同樣事物的另一種常見方式是說，“幾乎每個點都滿足P”或“幾乎每個x，P（x）成立”。

（1）如果屬性P近乎處處，並且隱含著屬性Q，那么屬性Q近乎處處。這取決於測度的單調性。

（2）如果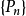

是一個有限或可數的屬性序列，每個屬性近乎處處，則它們的連線

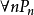也近乎處處。這取決於測度的可重複次數。

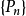
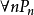
（3）相反，如果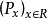

是不可數的屬性族，每個都保持近乎處處，然後它們的連線

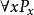不一定近乎處處。例如，若且唯若

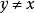，如果

是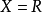

上的勒貝格度量並且

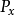是不等於x的屬性是真的，那么每個

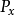近乎處處，但是

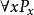不是近乎處處。

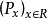
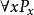
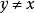
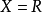
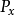
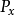
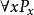
因為前兩個屬性，通常可以將測度空間的“幾乎每個點”理解為似乎是普通點而不是抽象點。這通常在非正式的數學論證中隱含地完成。然而，我們必須小心這種推理模式：對無數家庭聲明的普遍量化對於普通點是有效的，而不是“近乎每個點”。

（1）如果f：R→R是勒貝格積分函式，f（x）≥0近乎處處：

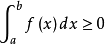
如果f（x）= 0近乎處處，那么對於所有實數a<b，上式都能取等號。

（2）如果f：[a，b]→R是單調函式，則f幾乎在任何地方都是可微分的。

（3）如果f：R→R是勒貝格可測度的，並且

對於所有實數a <b，則存在集合E（取決於f），使得如果x在E中，則勒貝格意味著

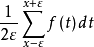
收斂到f（x），當

降到零。集合E被稱為勒貝格集合f。其補碼可以證明具有測度為零。換句話說，勒貝格的意思是f近乎處處。

（4）有界函式f：[a，b]→R是黎曼可積分，若且唯若它近乎處處連續。