將行列式D行的項轉為列的項成為行列式DT
則行列式DT稱為行列式D的轉置行列式
即行列式D行與列對換得到的新行列式DT
例如D第一行為a11、a12、a13···a1n
而DT第一行為a11、a21、a31···an1
基本介紹
- 中文名:轉置行列式
- 外文名:transposed determinant
- 相關詞條:轉置矩陣










































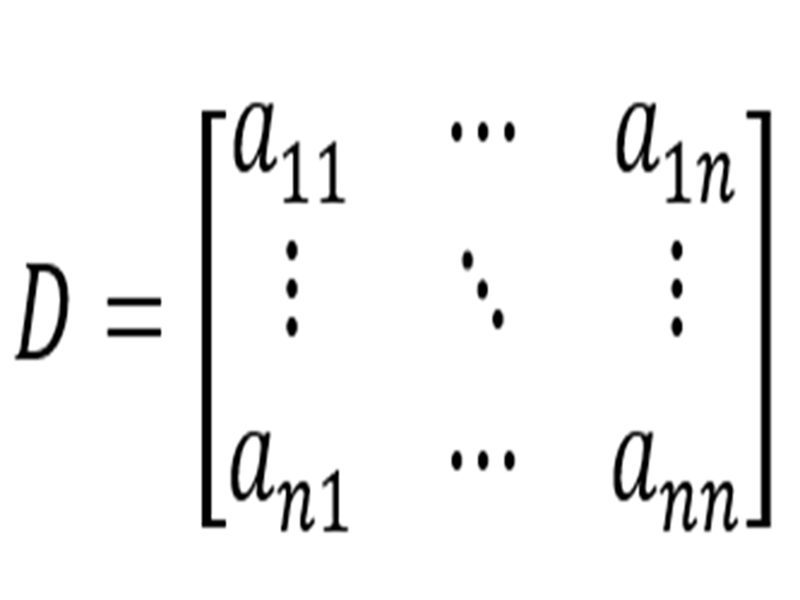
將行列式D行的項轉為列的項成為行列式DT
則行列式DT稱為行列式D的轉置行列式
即行列式D行與列對換得到的新行列式DT
例如D第一行為a11、a12、a13···a1n
而DT第一行為a11、a21、a31···an1










































將行列式D行的項轉為列的項成為行列式DT則行列式DT稱為行列式D的轉置行列式即行列式D行與列對換得到的新行列式DT例如D第一行為a11、a12、a13···a1n而DT第一行...
將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。... 將矩陣的行列互換得到的新矩陣稱為轉置矩陣,轉置矩陣的行列式不變。中文名 轉置矩陣 外文...
行列式在數學中,是一個函式,其定義域為det的矩陣A,取值為一個標量,寫作det(A)或 | A | 。無論是線上性代數、多項式理論,還是在微積分學中(比如說換元積分...
如右圖利用加減消元法,為了容易記住其求解公式,但要記住這個求解公式是很困難的,因此引入三階行列式的概念。記稱左式的左邊為三階行列式,右邊的式子為三階行列式的...
三角形行列式(triangular determinant)是一種特殊的行列式,包括上三角形行列式和下三角形行列式,亦稱上三角行列式和下三角行列式,統稱三角形行列式。每個行列式都可以只...
主對角線(從左上角到右下角這條對角線)下方的元素全為零的行列式稱為上三角行列式。一個n階行列式若能通過變換,化為上三角行列式,則計算該行列式就很容易了。....
n個未知數n個線性方程所組成的線性方程組,它的係數矩陣的行列式叫做係數行列式(determinant of coefficient)。...
行列式在數學中,是由解線性方程組產生的一種算式。行列式的特性可以被概括為一個多次交替線性形式,這個本質使得行列式在歐幾里德空間中可以成為描述“體積”的函式。...
線上性代數中,迪厄多內行列式是矩陣與除環和局部環上矩陣的行列式的推廣。 它是在1943年由迪厄多內提出的。...
