在計算機網路中, 路徑計算節點 (英語:Path Computation Element,PCE) 是能夠在來源和目的之間,發現並選擇可用路徑的組件、套用或網路節點。
基本介紹
- 中文名:路徑計算節點
- 外文名:Path Computation Element
詳情
路徑節點編碼的相關研究
路徑節點圓環編碼的設計
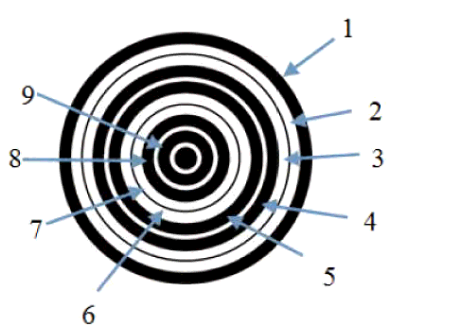 圖1
圖1 圖2
圖2Dijkstra算法
PCE 的擴展
- 域間 PCE 發現擴展
在計算機網路中, 路徑計算節點 (英語:Path Computation Element,PCE) 是能夠在來源和目的之間,發現並選擇可用路徑的組件、套用或網路節點。
 圖1
圖1 圖2
圖2在計算機網路中, 路徑計算節點 (英語:Path Computation Element,PCE) 是能夠在來源和目的之間,發現並選擇可用路徑的組件、套用或網路節點。...
用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。Dijkstra算法能得出最短路徑的最優解,但由於它遍歷計算的...
關鍵路徑法逆推法 活動和節點的最遲時間採用逆推法(Backward Pass)計算,逆推法(Backward Pass)一般從項目的最後一個活動開始計算,直到計算到第一個節點的時間為止,...
計算兩節點i與j間的節省值s(i,j)時,應先計算原路徑中各往返路徑的總和,再以之與較短路的總路徑和相比較;兩節點的原路徑與較短路,如下圖所示:...
,SPFA算法計算從 到圖中每個節點 的最短路徑。對於每個節點 ,從 到 的最短路徑表示為 。SPFA算法的基本思路與貝爾曼-福特算法相同,即每個節點都被用作用於鬆弛其...
路徑分析包含了兩個基本內容:一個是路徑的搜尋;另一個是距離的計算。路徑搜尋...該算法的基本思想是:認為兩節點間最佳路徑要么是直接相連,要么是通過其他已找到...
及其局部的障礙物分布情況,從而可以選出從當前結點到某一子目標結點的最優路徑...具有良好的全局最佳化能力、本質上的並行性、易於用計算機實現等優點,但計算量大、...
可以用同樣的步驟找出節點v1,v2,…等通向其餘各節點的最短路徑,編制出最小權數路由表。路徑選擇3.迂迴路由算法 在通信網中除了要求最佳路由之外,還須計算迂迴...
與傳統網路相比,感測器網路節點結構較為簡單,在儲存空間、 計算能力、頻寬、通信...算法根據相鄰城市間的關係對路徑進行變異,擴大蟻群的種群多樣性, 以便在算法停滯...
項目關鍵路徑步驟 編輯 1)畫出網路圖,以節點標明事件,由箭頭代表作業。這樣可以...4)當所有的計算都完成時,最後算出的時間就是完成整個項目所需要的時間。 5)...
的影響都不同;由於路由算法使用多種度量標準(metric),從而影響到最佳路徑的計算...連結狀態算法(也叫做短路徑優先算法)把路由信息散布到網路的每個節點,不過每個...
組播生成樹為數據組播時在網路里經過的路徑。MPH 算法是一種啟發式的求解近似最...1. [3] 集中算法(顯示路由算法、源路由算法):源節點計算出從源端到目標節點...
最短路徑問題是圖論研究中的一個經典算法問題,旨在尋找圖(由結點和路徑組成的)...有向圖或負權(但不可存在負權迴路)的最短路徑問題,同時也被用於計算有向圖...
當把起始原節點裝入堆疊後,此節點的對數似然函式就取為零。解碼算法包括下列步驟:1.計算其頂端節點的全部後繼節點的對數似然函式,並在堆疊適當的位置上把新的路徑...
是從一個頂點到其餘各頂點的最短路徑算法,解決的是有權圖中最短路徑問題。...目的是找到未訪問節點中d[j]值最小的那個節點, //作為下一個訪問節點,用k...
