趨勢檢驗是反映等級或生物學階梯關係的分類數據進行假設檢驗的有效方法,是由美國 Breslow 教授於1980年首先提出的。
基本介紹
- 中文名:趨勢檢驗
- 外文名:Trend Test
- 提出者:Breslow教授
- 出現年代:20世紀80年代
定義
分類
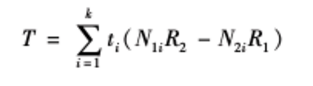

趨勢檢驗是反映等級或生物學階梯關係的分類數據進行假設檢驗的有效方法,是由美國 Breslow 教授於1980年首先提出的。
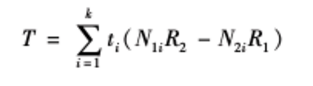
趨勢檢驗是反映等級或生物學階梯關係的分類數據進行假設檢驗的有效方法,是由美國 Breslow 教授於1980年首先提出的。...
世界氣象組織推薦並已廣泛套用的Mann-Kendall非參數統計方法,能有效區分某一自然過程是處於自然波動還是存在確定的變化趨勢。對於非常態分配的水文氣象數據,Mann-...
協整即存在共同的隨機性趨勢。協整檢驗的目的是決定一組非平穩序列的線性組合是否具有穩定的均衡關係,偽回歸的一種特殊情況即是兩個時間序列的趨勢成分相同,此時可能...
方差齊性檢驗(Homogeneity of variance test)是數理統計學中檢查不同樣本的總體方差是否相同的一種方法。其基本原理是先對總體的特徵作出某種假設,然後通過抽樣研究的...
趨勢投資法是以股票的上漲或下跌來作為股票買賣的依據,可以把股票作為籌碼進行操作,可以不考慮股票的業績支撐,當出現上漲趨勢時就買入,當出現下跌趨勢時就賣出。...
《順勢而為:道氏理論趨勢指標交易系統》是2011年中國宇航出版社出版的圖書,作者是時空老人。該書主要介紹了道氏趨勢指標交易系統的基本內容和使用方法。...
《和趨勢在一起》是2010年重慶出版社出版的圖書,作者是汪鄭武。... 在本書中,我們將AbleTrend置於嚴苛的市場眼光中接受檢驗。經事實證明,它可以幫助您對市場行為...
《食品檢驗新技術》根據國內外食品檢驗分析技術新的進展狀況及發展趨勢,系統地介紹了比較先進的食品分析方法和技術及較新的研究成果,重點闡述了幾項套用廣泛、影響...
方差分析(Analysis of Variance,簡稱ANOVA),又稱“變異數分析”,是R.A.Fisher發明的,用於兩個及兩個以上樣本均數差別的顯著性檢驗。 由於各種因素的影響,研究所...
(J反映了單調的趨勢,J越大單調趨勢越顯著) 類似的,遞減的檢驗為P(J≤c)=1-α(或構建Uij=(Xik>Xjl))。 當樣本足夠大時,構造Z近似於標準常態分配 (六)...
如果是選擇“用F檢驗的機率值”,越小代表這個變數越容易進入方程。原因是這個變數的F檢驗的機率小,說明它顯著,也就是這個變數對回歸方程的貢獻越大,進一步說就是...
(一)根據時間序列的散點圖、自相關函式和偏自相關函式圖以ADF單位根檢驗其方差、趨勢及其季節性變化規律,對序列的平穩性進行識別。一般來講,經濟運行的時間序列都...
