基本介紹
- 中文名:超彈性
- 外文名:hyperelasticity
- 含義:指材料存在一個彈性勢能函式
- 特點:卸載時應變可自動恢復的現象
- 學科:數理科學
- 類型:力學術語
定義
常見模型

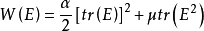



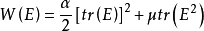

超彈性 (hyperelasticity) 是指材料存在一個彈性勢能函式,該函式是應變張量的標量函式,其對應變分量的導數是對應的應力分量,在卸載時應變可自動恢復的現象。應力和...
超彈性模型是指材料存在一個彈性勢能函式,常用來分析多孔結構材料的多孔介質力學模型。泡沫矽橡膠是一種具有高柔軟性、高延展性、高彈性並具有高孔隙度的多孔結構的...
正文超彈性物質指彈性物質的應力是某個勢函式對變形梯度的偏導數的物質。相應的勢函式稱為該物質的應變能函式或貯能函式。 詳見“純力學物質理論”詞條。 ...
偽彈性是指PE試樣被載入時,發生線性彈性變形之後,隨應力增加產生非線性彈性變形,卸載時,非線性彈性變形可以部分或完全恢復的現象。...
《合金的形狀記憶效應與超彈性》,是2002年1月1日國防工業出版社出版的圖書。...... 《合金的形狀記憶效應與超彈性》,是2002年1月1日國防工業出版社出版的圖書。...
書籍信息書名超彈性體非線性本構理論 書號978-7-118-08396-5 作者李忱 出版時間2012年09月 譯者 版次1版1次 開本32 裝幀 出版基金 頁數185 字數164 中圖...
註冊代理 保赫曼(上海)貿易有限公司 售後服務機構 保赫曼(上海)貿易有限公司 生產國(中文) 德國 產品名稱(中文) 超彈性固位繃帶中文名 超彈性固位繃帶 產品...
高階的非線彈性理論模型可表示為全量應力應變關係,也可以表示為增量應力應變關係,可以存在變形能函式,也可以不存在變形能函式。柯西彈性模型是建立在柯西彈性理論上...
《彈性與非彈性的測量和套用》是1999年冶金工業出版社出版的圖書,作者是李昕等。...... 1.3.6相變的影響與超彈性 1.4彈性與其他物理性能間的關係 2靜態彈性常數...
彈性力學的一個分支,又稱非線性彈性理論,是經典線性彈性力學的推廣。非線性彈性力學問題分為三類:物理線性、幾何非線性問題;物理非線性、幾何線性問題;物理非線性、...
viscoelasticity 流體的粘滯性及彈性的綜合性質。粘彈性聚合物在加工過程中通常是從固體變為液體(熔融和流動),再從液體變固體(冷卻和硬化),所以加工過程中聚合物於...
《NITI合金的超彈性力學特性及其套用》是2009年科學出版社發行處 出版的圖書,作者是王心美。本書是針對NiTi形狀記憶合金超彈性力學性能的一本專著,是NiTi形狀記憶...
彈性記憶(elastic memory)是指當溫度在某一很窄的範圍內可逆變化時,使材料的彈性模量的變化較大且具有可逆性的一種性質。...
《複合材料與粘彈性力學》是2011年2月1日機械工業出版社出版的圖書,作者是張少實。...... 主要闡述聚合物的粘彈性與屈服行為、材料的非線性粘彈性力學行為和超彈性...
形狀記憶合金(shape memory alloys,SMA)是通過熱彈性與馬氏體相變及其逆變而具有形狀記憶效應(shape memory effect,SME)的由兩種以上金屬元素所構成的材料。形狀記憶...
鎳鈦合金的相變偽彈性可達8%左右。 鎳鈦合金的超彈性可隨著熱處理的條件的變化而改變,當弓絲被加熱到400ºC以上時,超彈性開始下降。 3、口腔內溫度變化...
鎳鈦合金的相變偽彈性可達8%左右。 鎳鈦合金的超彈性可隨著熱處理的條件的變化而改變,當弓絲被加熱到400ºC以上時,超彈性開始下降。...
MiNiMA 眼鏡物料以歐洲優質β鈦為原料,鈦合金具有超彈性,永不變形的優點。材料考究,無焊接,去繁至簡的設計,線條幼細簡潔、流暢,做工精湛細緻,把鈦金屬的輕巧、...
幾何非線性行為:大位移,超彈性材料的大應變, 追隨力。包括邊界條件的非線性行為:結構與結構的接觸(三維滑移線),縫隙的開與閉合, 考慮與不考慮摩擦,強迫位移。...
“碰撞”在物理學中表現為兩粒子或物體間極短的相互作用。 碰撞前後參與物發生速度,動量或能量改變。由能量轉移的方式區分為彈性碰撞和非彈性碰撞。彈性碰撞是碰撞...
超彈性NiTi合金功能失效模型研究。功能材料,2015, 10(46), 10018-10022。(EI)[105]張茹遠,闞前華,康國政,張娟。形狀記憶合金增韌大塊金屬玻璃機理分析。複合材料...
