基本介紹
- 中文名:諧波小波轉換
- 外文名:Harmonic Wavelet Transform
- 領域:信號處理
- 定義:以小波為基底的線性轉換
- 結合:短時距傅立葉變換和連續小波轉換
- 提出時間 :1993年
基礎推理














一系列的諧波小波









低頻頻帶與正交












短時距傅立葉變換與連續小波轉換










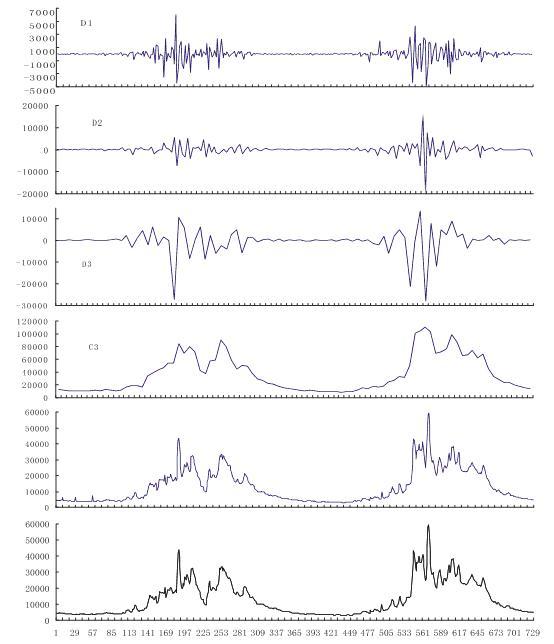













































諧波小波轉換(Harmonic Wavelet Transform)為學者大衛‧紐蘭德(David E. Newland)於1993年所提出,是一個以小波為基底的線性轉換,得以將信號變換至時頻域(Time-Frequen...
近年來基於小波分析的諧波檢測方法主要有基於 M allat 算法 、小波包變換 、連續小波變換( co ntinuous w avelet transform , CWT)復小波變換的諧波檢測方法等,這些方法都是基於小波變換的, 有各自的特點和適用場合 。基於 Mallat 算...
《小波變換理論及其在製造業中的套用》是2019年3月機械工業出版社出版的圖書,作者是[美]高曉暘(Robert X Gao)、嚴如強(Ruqiang Yan)。內容簡介 本書系統地介紹了從傅立葉變換到小波變換的歷史背景及相關數學基 礎, 深入淺出地...
《小波變換在電力系統中的套用》是2016年科學出版社出版的圖書,作者是蘇變玲。內容簡介 本書較全面地介紹小波變換在電力系統中的諧波檢測、暫態故障信號定位及雷電干擾的識別的基本原理和方法。全書共8章,主要內容包括:小波變換理論及其...
基於小波變換的診斷法。基於小波變換的診斷法由於在時域和頻域同時具有較好的局部化性質,克服了傅立葉分析法在非穩態信號分析方面的缺陷,更適用於對突變信號的分析。由於小波分析能計算出某一特定時間的頻率分布並把各種不同頻率組成的...
本項目擬在EWT理論的基礎上提出經驗諧波小波變換,廣義經驗小波變換和基於同步壓縮變換的時變模態分解等方法,並將EWT理論引入到機械故障診斷領域,建立系統的基於EWT理論的機械早期故障和變工況機械故障診斷新方法。項目研究成果對於小波分析...
主要內容包括:小波變換的開關電流技術實現基礎,小波變換的模擬濾波器綜合理論,小波函式的時域和頻域逼近,小波變換的單開關電流積分器實現,小波變換的級聯和多環反饋開關電流小波濾波器實現,小波變換電路在心電圖檢測、電力系統諧波檢測、...
第4章基於小波變換的隨機荷載模擬 4.1概述 4.1.1諧波疊加法 4.1.2線性濾波法 4.2平穩過程的隨機荷載模擬 4.2.1基於離散正交小波逆變換的平穩過程模擬算法 4.2.2風的基本特性描述 4.2.3算例 4.3非平穩過程的隨機荷載模擬 4...
全書共分七章,內容包括緒論、諧波分量數估計、基於最小二乘的諧波參數估計、基於疊代方法的諧波參數估計、基於小波分析的諧波參數估計、基於稀疏表示的諧波參數估計、基於盲源分離的諧波恢復。 《諧波信號分析與處理》可作為套用數學、信息...
測量分析公用電網供到用戶受電端的交流電能質量,其測量分析的指標:供電頻率偏差、供電電壓偏差、供電電壓波動和閃變、供電三相電壓允許不平衡度、電網諧波 套用小波變換測量分析非平穩時變信號的諧波。 測量分析各種用電設備在不同運行狀態...
當前套用到電力系統諧波分析中的人工神經網路模型有兩種,分別是多層前饋自適應人工神經網路模型和自適應線性人工神經網路模型。6、基於小波分析的諧波檢測方法 小波變換是數學發展史上的重要成果,套用十分廣泛,其在諧波檢測方面的研究成果也...
測量分析公用電網供到用戶受電端的交流電能質量,其測量分析的指標:供電頻率偏差、供電電壓偏差、供電電壓波動和閃變、供電三相電壓允許不平衡度、電網諧波 套用小波變換測量分析非平穩時變信號的諧波。 測量分析各種用電設備在不同運行狀態...
為此特引入視窗函式 ,並定義變換 。其中,a R且a≠0。該式定義了連續小波變換,a為尺度因子,表示與頻率相關的伸縮,b為時間平移因子。很顯然,並非所有函式都能保證上式中表示的變換對於所有f∈L²(R)均有意義;另外,在實際...
電力系統諧波的檢測方法 1.傅立葉變換諧波檢測法 在數字控制方面利用傅立葉變換進行李希特諧波檢測,將離散傅立葉變換所需要處理的是經過採樣和A/D轉換得到的數位訊號,確定電力系統諧波的屬性和特徵。2.小波變換諧波檢測法 對於高頻諧波...
來源文章摘要: 採用DASP小波分析模組,對反芻動物(綿羊、黃牛)的前胃各測點(瘤胃、網胃、網瓣口和瓣胃大彎)在4種生理狀態下(採食、食後、反芻和正常)的舒縮應變時域曲線進行小波分解,給出不同頻段諧波舒張和收縮應變幅值統計量,...
28.基於諧波小波變換的低速軸承故障診斷,軸承,2004.10 29.高線精軋機組軸承振動監測與故障分析,軸承,2004.5 30.基於FFT-FS頻譜細化及共振解調技術的電機軸承故障診斷,礦山機械,2004.3 31.可逆式軋機十字軸式萬向聯軸器輥端叉頭的...
離散正弦變換和離散餘弦變換的代數表征與描述;提出了SL(2,R)群上的諧波變換理論,並套用於圖像分析與表征;提出了分數階Fourier變換及諧波變換域的數字水印方法;結合分數階傅立葉變換的基本原理,提出了分數階小波變換的卷積理論;提出...
13.單相電路兩種諧波檢測方法的研究 《電子測量技術》 2010 05。14. 基於小波變換的電氣化鐵道牽引負荷諧波分析 《鐵道學報》 2011.06 (EI)。15. 基於MATLAB和小波變換的電力機車諧波電流分析 《電力自動化設備》,2012.01(EI)。承擔...
對連續周期型干擾濾波論及不多,小波變換對這類干擾應該也不是有效的。文[10]論及到連續周期型干擾濾波問題,它提出了3次B樣條小波對採樣信號進行預處理的方法,可基本消除偶次諧波和1.5次以上非整數次諧波。但這種方法對諧波濾波也...
