基本介紹
- 中文名:阻尼振動
- 外文名:damped vibration
- 別稱:減幅震動、衰減振動
- 定義:振幅隨時間減小的振動
能量損失
摩擦阻尼
輻射阻尼
動力學方程
振動方程
欠阻尼




過阻尼

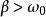
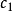

臨界阻尼
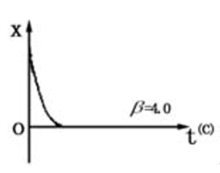

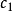


衰減振動一般指本詞條





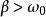
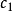



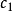

系統受初擾動後不再受外界激勵,因受到阻力造成能量損失而位移峰值漸減的振動。又稱阻尼振動。...
阻尼振動是指,由於振動系統受到摩擦和介質阻力或其他能耗而使振幅隨時間逐漸衰減的振動,又稱減幅振動、衰減振動。不論是彈簧振子還是單擺由於外界的摩擦和介質阻力總...
中文名稱 自由衰減振動法 英文名稱 free decay oscillation method 定義 通過測定試樣和慣性元件構成的組合件在初始扭矩作用下發生扭轉並隨即除去扭矩後其扭振振幅...
切削振動,指的是在用車床切削時候產生的振動。振動一旦加劇,會出現振幅超過幾十μm的激烈振動,通常還會伴隨很大的噪聲。在切削加工中,振動可能會超過100μm,此時...
系統中構件的彈性服從胡克定律,運動時產生的阻尼力與廣義速度(廣義坐標的時間導數)的一次式成正比的振動。...
瞬態振動是指由外加瞬態激勵引起的振動。瞬態過程是一種包羅萬象的非周期確定性過程,其基本特徵為持續時間較短的突發性過程,例如,飛機著陸,火炮發射,爆炸,地震,...
振動效應 (vibration effect ) 振動引起的人的生理和心理反應。振動可根據其對人體發生作用的部位,分為局部振動和全身振動;又可根據其對人體作用的方向分為與人體...
地基土體所受的動力作用,包括地震、機器振動、爆炸、打樁以及車輛行駛等。其中地震引起的振動,屬於不規則的、低頻的1~5Hz、有限次數的10~30次脈衝衰減振動,但其...
振動:描述系統狀態的參量(如位移、電壓)在其基準值上下交替變化的過程。狹義的指機械振動,即力學系統中的振動。電磁振動習慣上稱為振盪。腐蝕:廣義的腐蝕指材料與...
環境振動污染即振動超過一定的界限時,對人體的健康和設施產生損害,對人的生活和工作環境形成干擾,或使機器、設備和儀表不能正常工作。振動污染控制工程指減弱物體振動...
<1稱欠阻尼,物體作對數衰減振動;>1稱過阻尼,物體沒有振動地緩慢返回平衡位置。欠阻尼對系統的固有頻率值影響甚小,但自由振動的振幅卻衰減得很快。阻尼還能使受迫...
