莫雷角三分線定理,即任意△ABC每兩個內角相鄰的三等分角線的交點構成正△DEF.
基本介紹
- 中文名:莫雷角三分線定理
- 提出者:莫利
- 套用學科:數學幾何
- 適用領域範圍:平面幾何
定理定義,驗證推導,
定理定義
將三角形的三個內角三等分,靠近某邊的兩條三分角線相交得到一個交點,則這樣的三個交點可以構成一個正三角形。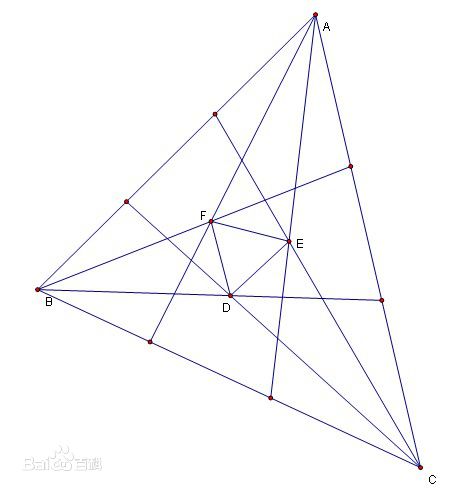

驗證推導
設△ABC中,AQ,AR,BR,BP,CP,CQ為各角的三等分線,三邊長為a,b,c,三內角為3α,3β,3γ,則α+β+γ=60°。
在△ABC中,由正弦定理,得AF=csinβ/sin(α+β)。
不失一般性,△ABC外接圓直徑為1,則由正弦定理,知c=sin3γ,所以AF=
(sin3γ*sinβ)/sin(60°-γ)=[sinβ*sinγ(3-4sin2γ)]/[1/2(√3cosγ-sinγ)]=
2sinβsinγ(√3cosγ+sinγ)=4sinβsinγsin(60°+γ).
同理,AE=4sinβsinγsin(60°+β)
∴AF:AE=[4sinβsinγsin(60°+γ)]:[4sinβsinγsin(60°+β)]=sin(60°+γ):sin(60°+β)=sin∠AEF:sin∠AFE
∴∠AEF=60°+γ,∠AFE=60°+β.同理得,CED=60°+α
FED=180°-CED-(AEF-α-γ)=180°-60°-α-60°+α=60
∴△FED為正三角形。
