莫比烏斯反演是數論數學中很重要的內容,可以用於解決很多組合數學的問題。
基本介紹
- 中文名:莫比烏斯反演公式
- 外文名:Möbius inversion formula
- 提出者:奧古斯特·費迪南德·莫比烏斯
- 套用學科:數學
- 適用領域範圍:數論
莫比烏斯反演的引入,莫比烏斯反演定理,莫比烏斯反演定理證明,莫比烏斯函式,莫比烏斯反演的性質,
莫比烏斯反演的引入
莫比烏斯反演是數論中的重要內容,在許多情況下能夠簡化運算。我們考慮以下求和函式:
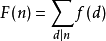
我們需要找到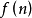 和
和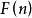 之間的關係。從和函式定義當中,我們可以知道:
之間的關係。從和函式定義當中,我們可以知道:
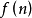
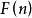

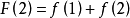
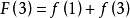

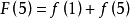
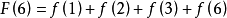
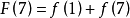
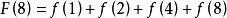
那么:
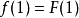
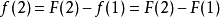

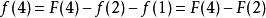

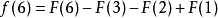
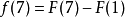
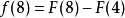
從中,可以看出,若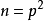 (
(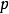 為質數)那么,
為質數)那么, ,所以,
,所以,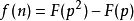 .
.
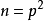
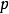

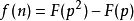
如果我們要讓函式滿足:
那么通過以上推導,我們可以知道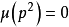 ,所以我們作出以下猜測:
,所以我們作出以下猜測:
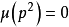
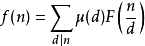
莫比烏斯反演定理
設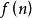 和
和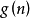 是定義在正整數集合上的兩個函式,定義如下。
是定義在正整數集合上的兩個函式,定義如下。
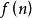
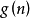
若函式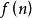 滿足:
滿足:
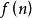
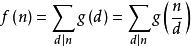
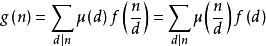
莫比烏斯反演定理證明
充分性證明:
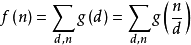
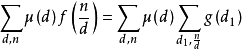

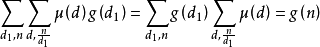
考慮到:
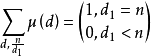
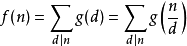
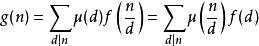
必要性證明:
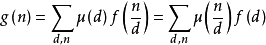
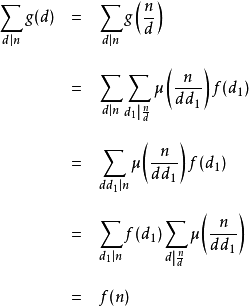
考慮到:
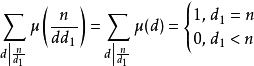
因此
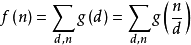
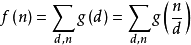

莫比烏斯函式
定義當 時,
時,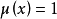

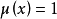
當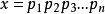 (
(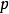 為不同的質數,且次數都為1),
為不同的質數,且次數都為1),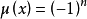
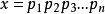
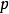
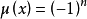
其餘情況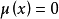
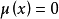
注意,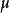 函式也為積性函式。證明略。
函式也為積性函式。證明略。
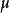
莫比烏斯反演的性質
性質一(莫比烏斯反演公式):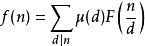
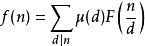
性質二:μ(n)是積性函式
性質三:設f是算術函式,它的和函式 是積性函式,那么 f 也是積性函式。
是積性函式,那么 f 也是積性函式。


