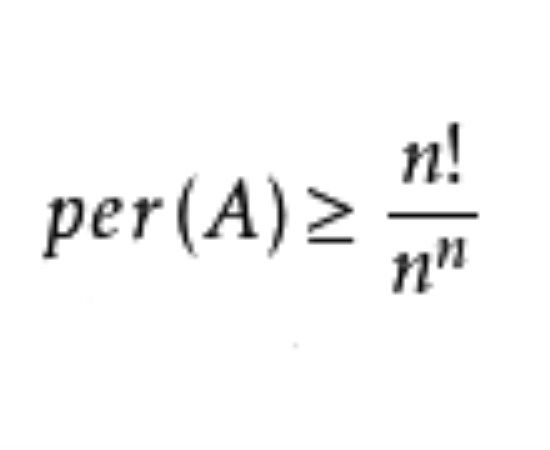范·德·瓦爾登猜想

范·德·瓦爾登猜想(Van der Waerden conjecture)是關於雙隨機矩陣積和式下界的一個估計，若一個n×n矩陣A的每個分量都是非負的，而且每個行和與每個列和都等於1，則稱A是一個雙隨機矩陣，設A為一個雙隨機矩陣，范·德·瓦爾登猜想是per A≥n!/n，並且等號成立若且唯若A的每個元素均為1/n。此猜想於1980年被蘇聯學者埃果里切夫(Г.П.Егорычев)所證實，其證明採用了其他數學家的一系列結果。

基本介紹

• 中文名：范·德·瓦爾登猜想
• 外文名：Van der Waerden conjecture
• 所屬學科：數學（組合學）
• 簡介：雙隨機矩陣積和式下界的一個估計
• 提出者：范·德·瓦爾登

基本介紹

范·德·瓦爾登(Van der Waerden)猜想是組合數學中關於正項行列式的一個極為重要的猜想。

設A是一個n行n列的矩陣，元素是a_ij，A的積和式定義為

求和遍及(1，2，…，n)的一切排列σ，其中，S_n表示n個符號的對稱群，A稱為雙隨機矩陣，是指它的每一行元素的和，每一列元素的和都等於1，則J_n是每個陣元都是的雙隨機矩陣。

在1927年，范·德·瓦爾登猜測：對於雙隨機矩陣A，成立著不等式

等號若且唯若，即時成立，這裡。這一猜測直到1984年前不久才被證明。

相關說明

1959年，馬庫斯和紐曼發表了關於范·德·瓦爾登猜想的第一篇論文，他們證明了在所有雙隨機矩陣的集合上，J_n是正項行列式函式的局部極小點，他們推導出使其正項行列式達到極小的雙隨機矩陣應滿足的性質，並對n=3的情形證明了這個猜想，此後，許多數學家寫了大量的文章對於n=4，n=5的情形。以及對許多特殊的類型的雙隨機矩陣證明了這個猜想。

在另一個方向上，班於1976年，而弗里德蘭(S.Friedland)於1979年彼此獨立地證明了對於任何雙隨機矩陣A有：

這個結果並不比范·德·瓦爾登的猜想弱多少，因為由斯特靈公式，近似等於。

現在范·德·瓦爾登猜想已經由兩位前蘇聯數學家獨立地解決了，一位是烏克蘭共和國建築業計畫與管理自動系統科學研究所的法利克曼(D.I.Falikman)，另一位是基雷斯基克拉斯諾雅茨克的蘇聯科學院西伯利亞分院的基雷斯基(L.V.Kirensky)物理研究所的埃戈里奇夫(G.P.Egorychev)。從時間上看是法利克曼先得到其證明，他早在1979年5月就把他的論文投寄給《數學註記》，而埃戈里奇夫一直到1980年末才散發他的論文的預印本，但法利克曼只是證明了范·德·瓦爾登定理，而埃戈里奇夫，另外還得到更強的結果：J_n是唯一的使正項行列式達到極小的雙隨機矩陣，雖然他們的證明在細節上有所差別，但都套用了亞歷山大德諾夫在1938年得到的一個關於二次型的混合判別式的不等式的特殊情形。

正如拉蓋里阿斯(J.C.Lagarias)所指出的那樣，范·德·瓦爾登猜想是一個富有挑戰性的問題，但是，這問題的解決並沒有給數學知識的現狀帶來革命性的變化，而要是黎曼猜想得到證明則肯定會這樣，然而，范·德·瓦爾登猜想肯定可以得出比以前更好的互不同構的拉丁方和斯坦納(Steiner)三元系的數目的下界，從長遠觀點看來，最有意義的結果是從關於二次型的混合判別式的亞歷山大德諾夫不等式以及與此有關的關於凸體的混合體積的亞歷山大德夫一芬切爾不等式可以推出大量的具有有趣組合解釋的多重線性不等式。