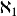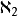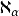在集合論中，阿列夫數，又稱艾禮富數，是一連串超窮基數。
基本介紹
- 中文名：艾禮富數
- 分類：數理科學
簡介,構造性定義,阿列夫,另見,
簡介
艾禮富數的標記符號為 ℵ （由希伯來字母א(aleph)演變而來）加角標表示。
可數集（包括自然數）的勢標記為
，下一個較大的勢為
，再下一個是
，以此類推。一直繼續下來，便可以對任一序數 α 定義一個基數
。
這一概念來自於康托爾，他定義了勢，並認識到無窮集合是可以有不同的勢的。
阿列夫數與一般在代數與微積分中出現的無限(∞) 不同。阿列夫數用來衡量集合的大小，而無限只是在極限的寫法中出現，或是定義成擴展的實軸上的端點。某些阿列夫數會大於另一些阿列夫數，而無限只是無限而已。
構造性定義
阿列夫數的直觀定義並沒有解釋什麼叫“下一個較大的勢”，也沒有證明是否存在“下一個較大的勢”。即便承認對任意的基數都存在更大的基數，是否存在“下一個較大的勢”使得這個基數和“下一個較大的基數”之間不再有其他的基數仍然是個問題。下面的構造型定義解決這個問題：
- ℵ0定義從前，它是一個良序集ℕ的序數；
- 考慮良序集按照某種同構關係劃出的等價類；
- 如上定義的等價類有一個特點：可比較，
設ℵa已定義且是一良序集的基數，考慮：
- 由於ℵa是某良序集的基數，這個良序集必存在於某個等價類中；一定還有其他基數為ℵa的良序集，這些良序集必將也存在於某個等價類中（可能與上面的同屬同一個等價類，但不一定）。所有這些等價類將做成一集，記為Z(ℵa)。
- Z(ℵa)也是良序集。
- 定義ℵa+1:= card(Z(ℵa))，它是一個良序集的基數。
阿列夫
是所有可數序數集合的勢，稱為ω1或有時為Ω。這個ω1本身是一個比所有可數序數更大的序數，因此它為一個不可數集。
在中國大陸，實數集的基數常被記為 c 或 ℵ，即 ℵ := ℶ1，這樣連續統假設就常常被表述為 ℵ = ℵ1．閱讀相關讀物時應避免混淆。人們在學數學分析（微積分）時常常以為自己時常遇到的是阿列夫數，事實上他們遇到的是 “ℵ”或“c”，即角標為1的ℶ 數。除非討論集合論，否則阿列夫數將是最不常用的基數之一。
另見
- 不可數集合
