基本介紹
- 中文名:脫穩
- 外文名:Destabilization
- 後續:凝聚
- 正文2:吸附電中和作用:膠體表
- 正文3:吸附架橋作用:如果投加
簡述
分類
壓縮雙電層
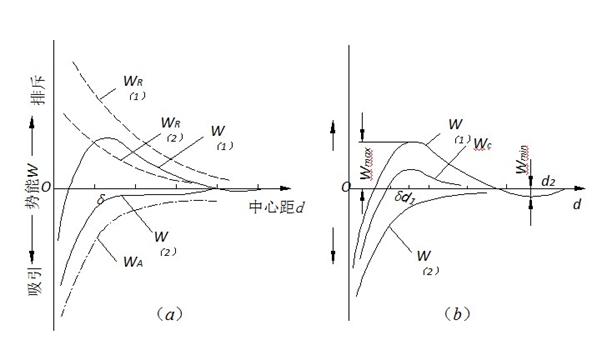
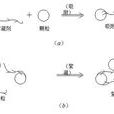
電性中和
吸附橋聯



膠體因 ζ 電位降低或消除,從而失去穩定性的過程稱為脫穩(Destabilization)。脫穩的膠粒相互聚集為微絮粒的過程稱為凝聚。不同的化學藥劑能使膠體以不同的方式脫穩...
粒子脫穩destabilisation of particles膠體顆粒失去穩定性的過程稱為脫穩。脫穩過程可通過以下兩種作用完成,其一,使膠核外擴散層厚度減小,縮短膠核間距離,增加范德華...
混凝法就是向廢水中投放混凝藥劑,使其中的膠體粒子和細微懸浮物脫穩,並聚集為數百微米以至數毫米的礬花,進而可以通過重力沉降或其他固液分離手段予以去除的廢水處理...
水力條件是影響混凝過程中的關鍵性因素之一,水力條件影響混凝劑在水中的擴散,混凝劑加入原水中後將進行混合與擴散及混凝劑水解,水解產物與膠體顆粒作用使其脫穩而從...
凝聚主要指膠體脫穩並生成微小聚集體的過程,絮凝主要指脫穩的膠體或微小懸浮物聚結成大的絮凝體的過程。影響混凝效果的主要因素:(1)水溫:水溫對混凝效果有明顯的...
當向水中投加帶相反電荷的膠體後,水中膠體顆粒與加入的相反電荷的膠粒之間發生電性吸附和電性中和作用,使兩種膠體顆粒的ζ電位都降低或消失,從而發生脫穩凝聚作用。...
常規混凝的絮凝體形成過程,是一個脫穩顆粒間隨機碰撞結合的過程,形成的絮凝體結構鬆散,內部空隙率大、密度低、沉降速度慢,在大量高濁度水淨化試驗研究和分析基礎上,...
絮體是又稱礬花。水中膠體顆粒通過加入混凝劑脫穩後,相互接觸聚集形成的一種絨毛狀固體物。...
含油污水處理鹽析法基本原理是壓縮油粒於水面界面處雙電層的厚度,使油粒脫穩。單純鹽析法投藥量大(1%~5%),聚析的速度慢,沉降分離一般在24h以上,設備占地面積大,...
是投加形成絮凝體的化學藥品,使膠體的或微細懸浮物質發生脫穩作用和初始聚集。投加入水中的化學藥品,或與正常存在於水中的物質,或與為了進行化學沉澱而加入水中的...
