胞腔逼近定理(cellular approximation theorem)是代數拓撲學的一條重要定理。與單純逼近類似，CW復形之間的連續映射可以用胞腔映射來逼近。
基本介紹
- 中文名：胞腔逼近定理
- 外文名：cellular approximation theorem
- 領域：數學
- 學科：代數拓撲學
- 類似：單純逼近
- 映射：連續映射
概念,逼近定理,代數拓撲學,連續映射,
概念
胞腔逼近定理(cellular approximation theorem)是代數拓撲學的一條重要定理。與單純逼近類似，CW復形之間的連續映射可以用胞腔映射來逼近。相對CW復形之間的連續映射：f： (X，A)→(Y，B)，稱為胞腔的，若對於每個n≥-1，f((X，A)n)
(Y，B)n。胞腔逼近定理斷言：相對CW復形之間的任何連續映射f：(X，A)→(Y，B)都相對於A同倫於一個胞腔映射，並且相對於A同倫的任何兩個胞腔映射的同倫都可以通過一個胞腔同倫來做到。
逼近定理
逼近定理是不同的賦值之間相互獨立的定理，是中國剩餘定理(孫子定理)的推廣。該定理斷言：若φ1，φ2，…，φn是域F的互不等價的非平凡賦值，a1，a2，…，an為F中任意元素，則對於任意ε>0，總存在F中元素x使φi(x-ai)<ε對i=1，2，…，n均成立。
逼近定理揭示出不等價的有限個賦值是相互獨立的，這是孫子定理的推廣，在處理多個賦值時將很重要。
現若
為有理數域，
是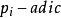
賦值，相應指數賦值記為
對任意
任取
，則由上述定理有x使
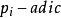
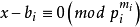
代數拓撲學
早期所稱的組合拓撲學，是19世紀末彭加勒 (H.Poincare，1854～1912) 首先提出的，在1895～ 1904年間他創立了用剖分研究流形的基本方法，並 引進了許多不變數——基本群、同調、貝蒂數、撓 係數，並提出了具體的計算方法。他探討了三維流形 的拓撲分類問題，提出了著名的彭加勒猜想。繼後， 布勞維爾 (L.E.Brouwer，1881～1966) 在1910～ 1912年間提出了用單純映射逼近連續映射的方法， 並證明了不同維歐氏空間不同胚，開創了不動點類理 論，使組合拓撲學在概念精確、論證嚴密方面達到了 應有的標準。緊接著亞歷山大 (J.W.Alexander， 1896～) 於1915年證明了貝蒂數與撓係數的拓撲不 變性。隨著抽象代數學的興起，1925年前後，經諾 特 (A.E.Noether) 提議，H.霍普夫於1928年將組 合拓撲學建立在群論基礎上，定義了同調群。從此組 合拓撲學逐步演變成利用抽象代數的方法研究拓撲問 題的代數拓撲學。
代數拓撲學的基本思想是： 對一個拓撲空間聯繫 一個或一列代數系統; 對空間之間的連續映射，聯繫 相應的代數系統之間的同態，以此反映空間與映射的 拓撲性質。代數拓撲學的內容主要有：①同調論。研究與同調概念有關的課題，如單純同調群、奇異同調群，上同調群及同調論公理、範疇與函子；②同倫論。研究與連續映射的連續形變有關的各種課題，如同倫問題、提升問題、同倫分類問題及同倫群的計算問題、倫型問題、不動點類理論。目前代數拓撲學已成為十分重要的數學分支，它的發展深刻地影響著其它數學分支，甚至在理論物理與原子核構造的研究中也得到了廣泛套用。
連續映射
設f為從拓撲空間E到拓撲空間F中的映射。 稱f在E的點x0是連續的，如果對f(x0)在F中的任一鄰域W，在E中存在x0的鄰域V，使在f下V的象包含在W中；換言之，如果在f下f(x0)的任一鄰域的逆象是x0的鄰域。
稱f在E上是連續的(或簡稱f是連續的)，如果它在E的每一點都連續。
為使f是連續的，必須且只須F的任一閉集經由f的逆象是E的閉集，或F的任一開集經由f的逆象是E的開集。但是E的開集(閉集)經由連續映射的正象不一定是F的開集(閉集)。
從E到F中的常映射是連續的.E的恆等映射是連續的。
任一從離散空間到拓撲空間的映射是連續的。
設E，F及G為拓撲空間，f為從E到F中的連續映射，而g為從F到G中的連續映射，則複合映射g°f是連續的。
當E與F為分別賦以距離d及e的度量空間時，為使f在x0點連續，其充分必要條件是：對任一嚴格正的實數ε，存在嚴格正的實數η，使得由關係d(x，x0)≤η可推出e(f(x)，f(x0))≤ε。若f為定義在R的子集P上的有限數值函式，則使f在x0點連續的充分必要條件是：對任一嚴格正的實數ε，存在嚴格正的實數η，使得對P的任一元素x，關係|x-x0| ≤η蘊涵|f(x)-f(x0)|≤ε。
