置信係數(confidence coefficient) 亦稱“信度係數”、“置信機率”或“置信度”:即被估計的總體參數落在置信區間內的機率D,以1-a表示,用以說明置信區間的可靠程度。置信係數的選擇一般由研究者根據對區間估計的可靠程度的要求而定,通常選用的置信係數為0.95和0.99。置信係數增大,置信區間的長度相應增加。
基本介紹
- 中文名:置信係數
- 外文名:confidence coefficient
- 別稱:信度係數、置信概、置信度
- 作用:說明置信區間的可靠程度
- 所屬學科:數學
定義,定義一,定義二,置信係數計算,作用,
定義
定義一
置信係數又稱“置信機率”、“置信度” “信度係數”。系區間估計中,使估計的總體參數落在置信區間的機率,即式


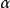

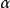




定義二
在套用機率的方法估計實驗誤差時,經常使用置信係數這個概念,它的定義是:遵從一定機率分布的某項誤差對應於所給置信機率的誤差限與標準差之比,叫做該項誤差的置信係數。若用K表示置信係數,e表示誤差限, 表示標準差,則有定義的數學表達式
表示標準差,則有定義的數學表達式


從物理意義上來理解,就是說一項誤差的機率分布確定之後,標準差即確定,對應於所給置信機率( )的誤差限也就確定了,該誤差限可以用標準差乘以一個係數來表示,這個係數就是置信係數。
)的誤差限也就確定了,該誤差限可以用標準差乘以一個係數來表示,這個係數就是置信係數。

可見,置信係數是描述對於某一個置信機率情況下標準差和誤差限(或置信限)之間關係的一個量,它的大小不但與置信機率有關,而且與機率分布有關。
置信係數計算


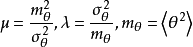







在誤差合成中,往往運用廣義方和根法來計算總不確定度u,即











作用
置信係數在誤差合成中有較大的作用,主要為以下兩方面:
i)對於各項未定系統誤差,利用各自機率分布的置信係數,可以很方便地進行 與e之間的換算,有利於採用較好的廣義方和根法進行誤差合成。
與e之間的換算,有利於採用較好的廣義方和根法進行誤差合成。

ii)對於已求得的標準差,乘以置信係數即可得到不確定度(或誤差限),置信係數選得過大,誤差限就大幹客觀誤差限,顯得保守;反之就冒險,因此,應該根據誤差的機率分布和需要的置信機率來合理選取。使誤差合成結果儘可能符合實際情況。