主纜的結構
早期,在歐洲和美洲,懸索橋的主纜曾採用過眼桿,其主要優點是可以適應纜力沿橋變化而改變截面,用料經濟。1931年,在巴西建成的佛羅里亞諾波利斯(Florianopolis)橋,是跨度為129+340+129(m)的懸索橋,其主纜中段和加勁樑上弦合成一體,其經濟性更加明顯。隨後,美國也曾經修建幾座這種樣式的懸索橋。但這種用眼桿作主纜的懸索橋有一致命弱點,那就是某一眼桿其淨截面裂通會導致全橋破壞、甚至墜毀。所以,隨著工業技術的發展,懸索橋主纜多採用抗拉強度和疲勞強度更高的鋼絲。此時,為了施工方便,中、小跨度懸索橋多使用鋼絞線。但是,鋼絞線的彈模低,使得橋的變形增大;且鋼絞線作主纜時不易按設計截面形狀壓緊、也難採取有效的防腐措施。所以,大跨懸索橋主纜又多採用平行鋼絲來製作。
主纜的材料
在設計懸索橋時,其主纜材料要求的條件可按以下考慮:①材料單位有效面積的抗拉強度大;②材料拉伸的延伸率小;③材料彈性模量大;④材料截面密度大;⑤材料
疲勞強度高、
徐變小;⑥方便主纜製作;⑦製成主纜後其
錨固和防鏽容易;⑧材料價格便宜。以上8條要求,可隨各橋的具體情況和重要程度而異,所以在懸索橋主纜設計中必須綜合地考慮。
主纜的類型
在懸索橋主纜的設計中,多是根據上述材料要求條件而選擇主纜的類型。而主纜類型主要有如下兩類:①鋼絲繩主纜,多用於中、小跨懸索橋中,它又分為鋼絞線繩和螺旋鋼絲繩(Spiral rope又簡稱SPR)、封閉式鋼絞線索(Locked coil rope又簡稱LCR);②平行絲股主纜,主要用於大跨懸索橋,根據製作方法分為空中繞線法的平行絲股主纜(Air spinning method又簡稱AS)和預製絲股法平行絲股主纜(Shop—fabricabled parallelwire strand method又簡稱PWS或PS)兩種。
一些懸索橋主纜設計參數可以從其他的設計手冊上查到。一般來說,鋼絲繩主纜僅用於600m以下跨度的懸索橋,而平行絲股主纜用於跨度在400m以上的懸索橋。當懸索橋跨度在400~600m範圍,鋼絲繩主纜和平行絲股主纜兩者的經濟性基本相同。設計中可根據其具體情況考慮採用。
主纜的結構型式
大多數懸索橋都採用雙面主纜,但也有單面主纜者。至於主纜的根數,一般是一側布置一根。但因主纜太粗、架設困難或者工期限制等原因,也有一側用兩根主纜的設計。若在橋的每側都用兩根主纜,並且兩主纜在立面的幾何形狀不同,這就稱為複式主纜。它以跨中為界,一纜的曲率在跨中的這一側較大,在另一側較小;而另一纜的曲率分布就和它相反。這樣,當單跨加活載時,在該半跨中曲率較大的那一根主纜當承擔較大活載時,這就有利於減小撓度,並減小加勁梁的彎矩。這對大跨懸索橋尤為重要。
如上所述,懸索橋主纜設計多採用平行絲股,而根據其製作方法的不同分成預製絲股(PWS)和空中繞線(AS)兩種。對有隧道式錨碇墩的或特大跨的懸索橋,採用空中繞線法或許更為有利。
懸索橋主纜絲股外形多按六角形配置,一般有尖頂型和平頂型兩種,見下圖。
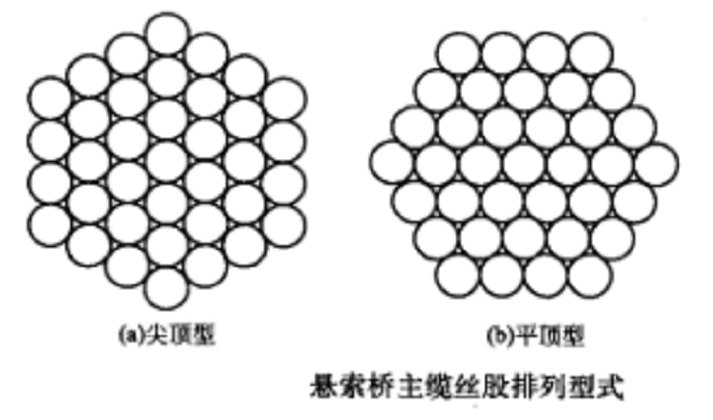 懸索橋主纜絲股排列型式
懸索橋主纜絲股排列型式主纜的設計
主纜幾何線形的確定
(1)主纜矢跨比的選擇
懸索橋主纜的矢跨比直接影響懸索橋的整體剛度。選擇較小的矢跨比有利於提高全橋的剛度,但會相應增大主纜的拉力,從而有可能使得同一荷載條件下的主纜面積需相應增大。一般情況下懸索橋的矢跨比在1:9~1:10左右。
(2)主纜的成橋線形計算
主纜成橋線形的幾何計算,首先依據橋樑的縱斷面線形,求出控制主纜幾何線形基本點的位置,計算圖示見下圖。
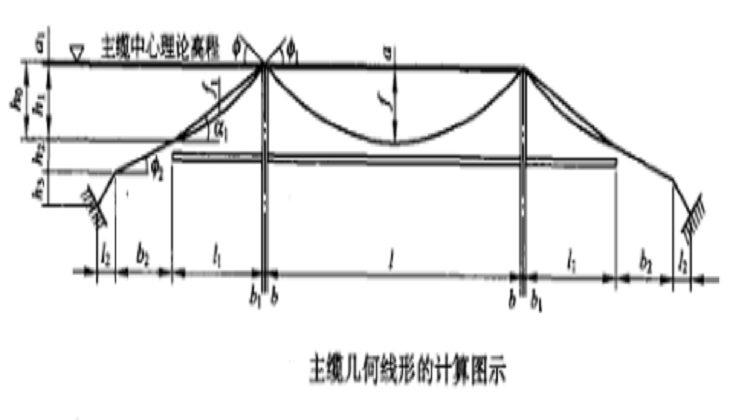 主纜幾何線形的計算圖示
主纜幾何線形的計算圖示先求邊跨矢高
,根據主纜在塔頂處恆載水平拉力相等可以得出:
塔頂主纜中心線理論高程:
=(跨中主纜中心線高程+
+
)-岸側跨端主纜中心線高程
至此,控制主纜幾何線型的基本點均已確定,再根據錨碇方式就可以確定
、
等數值。
主纜截面設計
架設主纜設計成由10010根φ5mm的鍍鋅高強度鋼絲組成,其設計面積為
。10010根鋼絲分成110股平行鋼絲束,每束91根鋼絲。主纜架設時,先將110股預製平行鋼絲束編排成六角形截面,再擠成圓形。截面擠緊的空隙率在一般部位按20%考慮,其相應的外徑為570mm左右,在安裝索夾的部位由於索夾的緊固作用,空隙率將壓縮至18%左右,此處主纜的外徑約為560mm,見下圖。
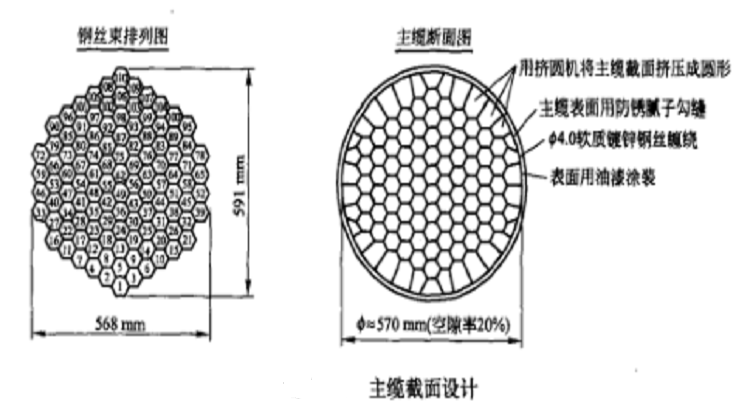 主纜截面設計
主纜截面設計每股預製的平行鋼絲束由91根直徑為5.1mm的鍍鋅鋼絲組成六角形截面。這樣設計的截面具有截面緊湊、幾何穩定性好、便於編束定位和方便施工等優點。為保持預製平行鋼絲束的截面形狀,沿長度方向每隔1.5m用特殊纖維強力膠帶將鋼絲束包紮定型。
如下圖所示,在六角形截面的右上角設有一根噴塗紅色油漆的觀察鋼絲,其作用是在製作和架設鋼絲束過程中用以觀察、辨別鋼絲束是否發生扭轉。在截面的左上角設有一根標準長度鋼絲,此鋼絲是每股預製平行鋼絲束下料長度和標塗各標記點(如塔頂鞍座中心、跨中中點等部位)的依據,它是預先將鋼絲展開伸直並通過精密測量刻記後製成的。根據國外的有關規定,標準長度鋼絲的長度誤差應小於1/36000。
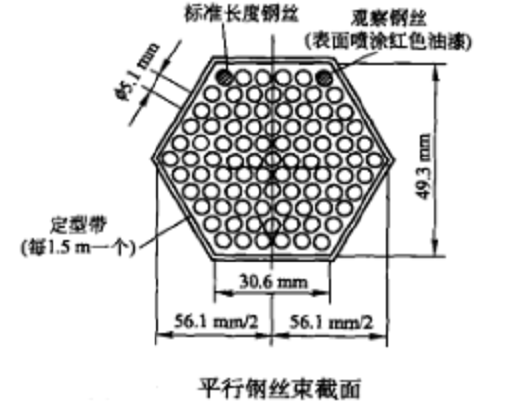 平行鋼絲束截面
平行鋼絲束截面鋼絲束無應力長度的計算
鋼絲束無應力長度系指鋼絲束兩端錨頭前支撐面問無應力狀態下的長度,此長度計算準確與否直接關係到懸索橋主纜幾何線形的精確程度。
鋼絲束無應力長度的計算以成橋狀態下標準溫度為20℃時,主纜的設計幾何線形為依據,先求出成橋狀態下主纜鋼絲束的幾何長度,然後扣除一、二期恆載作用下主纜鋼絲束產生的彈性伸長量,從而得到自由懸掛狀態下的懸鏈線長度,此長度再扣除由鋼絲束自重產生的彈性伸長量,即可得到鋼絲束的無應力長度。
懸索結構:集中荷載
在全纜索處於受載後的平衡狀態時,它的反力發生在纜索的支承處。纜索自身對支承處施加的力一般都是向內、向下作用的,而其基礎提供的反力則和纜索自身內力在數量上相等在方向上相反。在通常情況下,不可能只用考慮全纜索平衡的辦法算出反力。因為纜索的反力一般是用它的水平反力和豎向反力表示的,由於每個反力都有兩個分力,這樣就有了4個未知力,但只有3個獨立的靜力方程式求解,這就必須考慮纜索結構的一個隔離體才能求出全部反力。下面將闡明這種辦法。
伴隨求反力的另一任務是確定纜索的準確幾何形狀。受載纜索的準確形狀取決於荷載條件,它不可能由設計人事先任意給定。設計人可以預先指定一個最大垂度或其他某個數值,但這些不是纜索自身的準確形狀。而尋求纜索的準確形狀正是對纜索結構進行分析過程中的一個基本目的。
纜索構件中的內力永遠處於純受拉狀態。因為一條纜索可以想像為由一個連續系列的分散單元互相鉸接地連線在一起形成的——這顯然就是一根鏈條。這種情況下,每一個分散單元在任一荷載作用下都可以自由轉動,它也就使得局部的內彎矩不能由一個單元傳遞給另一單元。於是,由內力和外力在纜索任意一處產生的所有轉動效應之總和必為零(這就是構成計算纜索幾何形狀和反力所用方法的原理,下面將予以敘述),因此,纜索中存在的內力必然處於純受拉狀態。如果這時纜索的準確幾何形狀已知或設法加以假定,那么其內力的大小就可以用一個類似求桁架內力的節點平衡法的途徑計算出來(纜索上任一點在該點所有內力和外力作用下,在豎向和水平方向都必須當然地處於平衡狀態)。
任何結構的功能都可以定義為承受施加荷載效應後所產生的外剪力和外彎矩。在一個纜索或索形拱結構中,其任一載面上的外剪力是由該截面軸向內力的豎向分力所提供的內部抗剪力相平衡的;對於該截面的總外彎矩,則是由該截面軸向內力水平分力和該結構端支承處水平反力形成力偶所提供的內抵抗彎矩相平衡的。這裡的水平反力可以是基礎處發生的水平推(拉)力,也可以分別是拱結構或纜索結構端支承點之間拉桿或壓桿的內力。
 懸索橋主纜絲股排列型式
懸索橋主纜絲股排列型式 主纜幾何線形的計算圖示
主纜幾何線形的計算圖示














 主纜截面設計
主纜截面設計 平行鋼絲束截面
平行鋼絲束截面
