線性正則變換(Linear canonical transform,LCT)是一種更加廣義的積分變換,Fourier變換、分數階Fourier變換以及Fresnel變換等都可以看成線性正則變換的特殊形式。LCT具有三個自由參數(參變數之間存在一個約束條件,使得具有四個參變數的線性正則變換實際上只有三個自由參數),故擁有更大的靈活性。
基本介紹
- 中文名:線性正則變換
- 外文名:linear canonical transform
- 簡寫:LCT
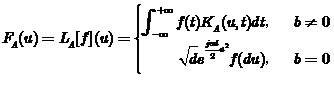
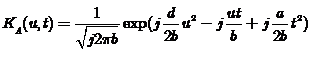
 圖1線性正則變換的幾何表示
圖1線性正則變換的幾何表示線性正則變換(Linear canonical transform,LCT)是一種更加廣義的積分變換,Fourier變換、分數階Fourier變換以及Fresnel變換等都可以看成線性正則變換的特殊形式。LCT具有三個自由參數(參變數之間存在一個約束條件,使得具有四個參變數的線性正則變換實際上只有三個自由參數),故擁有更大的靈活性。
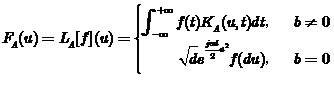
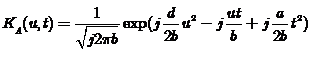
 圖1線性正則變換的幾何表示
圖1線性正則變換的幾何表示線性正則變換(Linear canonical transform,LCT)是一種更加廣義的積分變換,Fourier變換、分數階Fourier變換以及Fresnel變換等都可以看成線性正則變換的特殊形式。LCT具有三個自由參數(參變數之間存在一個約束條件,使得具有四個參變數的線性...
《線性正則變換及其套用》是2013年2月1日科學出版社出版的圖書,作者是許天周、李炳照。內容簡介 本書著重以線性正則變換的基本理論與初步套用為出發點,系統論述了線性正則變換的基本數學原理及其與信號分析與處理領域相關的一些基本概念,...
全書共9章,內容包括線性正則變換基礎理論、線性正則變換域帶限信號採樣理論、連續線性正則變換域帶限信號外推、離散線性正則變換域帶限信號外推、基於含噪聲樣本的線性正則變換域帶限信號重構、廣義4f光學系統及其本徵問題、廣義4f光學系統...
具體研究情況和成果如下: (1)以線性正則變換的基本理論及套用為出發點,探討了多項式Fourier變換的基本理論與方法。研究線性正則變換域的採樣理論,提出了多項式變換域模糊函式與魏格納分布的全新定義,建立了二維經典魏格納分布與二維多項...
全書共分為13章,各章內容均緊緊圍繞分數階傅立葉變換這一主題,包括:定義和性質、採樣及數值計算、分數階傅立葉域濾波、隨機信號和陣列信號處理、雷達和通信中的套用、圖像處理、線性正則變換等。編輯推薦 《分數階傅立葉變換及其套用...
主要包括:(1)代數信號處理的基本理論研究:研究採樣、濾波、頻譜回響等信號處理的基本概念在代數信號處理體系下的表征;探索現有信號處理變換理論(Fourier變換、小波變換、分數階Fourier變換、線性正則變換等)的代數表征與描述;(2)代數...
李炳照,男,1975 年生,博士,北京理工大學數學學院副教授,碩士生導師。主要從事小波變換、分數階Fourier 變換、線性正則變換等新穎數學方法的基本理論及其在非平穩信號分析與處理中套用研究。人物經歷 1998年畢業於山東師範大學數學系獲理學...
4、利用建立在特殊線性群上的線性正則變換理論,研究圖像水印問題。我們在研究圖像水印時參數的選擇多了靈活性,適當的參數選擇使得圖像水印比已有的方法效果更好。 5、完成了專著《信息幾何導引》,系統地介紹了信息幾何的基本內容。 6、...
3.4.1 希爾伯特變換 / 90 3.4.2 固有時間尺度分解方法 / 96 3.4.3 冗餘小波變換 / 99 3.4.4 線性正則變換 / 102 參考文獻 / 110 第4章 系統運行異常工況識別 / 111 4.1 概述 / 111 4.2 基於統計分析的...
向量場正則形理論突破了傳統穩定分析的局限,把模式和大幹擾下系統的動態特性聯在了一起,而在電力系統中套用向量場正則形理論的關鍵是求解出非線性正則變換係數。本文提出了數值求解向量場非線性正則變換係數的算法(ND算法),該算法簡單...
