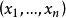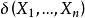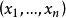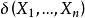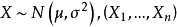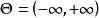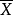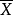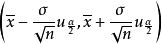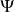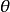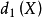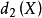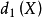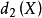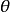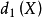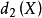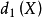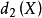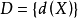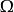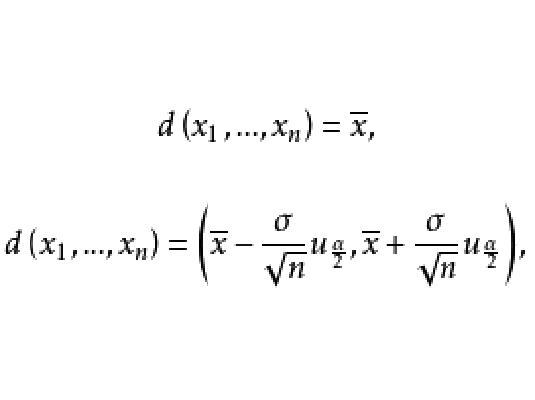統計決策函式

統計決策函式(statistical decision function)亦稱判決函式，是統計決策理論的基本概念之一。統計推斷的任務就是建立一個定義於樣本空間X上，取值於決策空間D內的函式δ(x)，使當有了樣本X時，就採用判決δ(x)，這種函式稱為非隨機化的統計決策函式。若對每個樣本X，有決策空間(D，B_D)上的機率測度δ*(x)與之對應，則稱δ*(x)為隨機化的決策函式。通常，決策函式是指非隨機化的決策函式。

基本介紹

• 中文名：統計決策函式
• 外文名：statistical decision function
• 別名：判決函式，決策函式
• 所屬學科：數學（統計學）
• 相關概念：樣本空間，統計決策問題等

基本介紹

對於一個統計決策問題，可以從樣本空間到決策空間建立一個對應規則，可看作定義在樣本空間上，取值於決策空間內的函式，稱其為統計決策函式。

給定了一個統計決策問題，即給定了一個參數統計模型(樣本空間及樣本的分布族)、決策空間與損失函式，自然希望對樣本空間中的每一個點指明一個決策，這樣一個規則是定義在樣本空間上，取值在決策空間上的一個函式，稱這個函式為(統計)決策函式，記作。在不致引起誤解的情形下，也稱為決策函式，它表示在得到樣本觀測值時，採取決策。易見，本質上是一個統計量。 決策函式是所給定的統計決策問題的一個解。

例1 總體是總體X的一個樣本，為未知參數，參數為已知。參數空間為。在點估計中，用樣本均值作為的估計量，所以，關於的每一個取值都代表一個對參數的決策，統計決策空間為。在區間估計中，若採用置信區間，則區間代表一個對參數的決策，統計決策空間為

其中，。值得注意的是，在中具體選取哪個決策與抽取的樣本和所採用的統計方法有關。

在次例的點估計中，統計決策函式為

在區間估計中，統計決策函式為

也稱為統計決策函式。它可看成在得到樣本觀測值時，

採取決策，實質上，統計決策函式是一個統計量。

統計決策函式的風險函式

給定一個決策函式之後，所採取的決策依賴於樣本觀察值，對應的損失函式也依賴於樣本觀察值。觀察值不同，所採取的決策不同，對應的損失函式也不同。因此，不能依賴樣本的一次觀察值所採取的某個決策而帶來的損失來衡量決策的優劣，而要從總體上來評價。一個常用的數量指標是平均損失，稱

為決策函式的風險函式。

決策函式的風險函式表示當參數值為時，採取決策d所產生的平均損失。風險越小，損失越小，決策函式就越好。當決策函式給定時，風險函式是的函式。比較兩個決策函式和的優劣，可通過比較其風險函式。

等價決策函式

設和是統計決策問題中的兩個決策函式，對任意，如果其風險函式滿足不等式

且存在一些，使上述嚴格不等式成立，則稱決策函式一致優於。對任意，如果其風險函式滿足等式，則稱決策函式等價於。

一致最小風險決策函式

設是一切定義在樣本空間上取值於決策空間上的決策函式的全體，如果存在一個決策函式，使對任意和對任意，都有

則稱決策函式為一致最小風險決策函式或一致最優決策函式。

等價決策函式和一致最小風險決策函式都是對同一個給定的損失函式而言的，損失函式不同，相應的結果也隨之改變。