與一元函式的極限相類似,二元函式的極限同樣是二元函式微積分的基礎。但因自變數個數的增多,導致二元函式的極限要比一元函式的極限複雜很多。求累次極限實質上是求兩次一元函式的極限,因此,累次極限又稱二次極限。需要注意的是:累次極限與重極限是兩個不同的概念,它們的存在性沒有必然的蘊含關係。
基本介紹
- 中文名:累次極限
- 外文名:repeated limit
- 學科:數學
- 領域範圍:數學分析
- 屬性:二元函式的極限與連續
定義和例子,定義1,例1,例2,重極限與累次極限之間的聯繫,定理1,推論1,推論2,
定義和例子
定義1
設 ,
, 在
在 軸、
軸、 軸上的投影分別為
軸上的投影分別為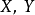 ,即
,即




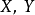


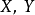
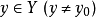





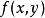
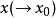




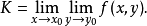
對於兩個自變數 同時以任何方式趨於
同時以任何方式趨於 ,即
,即


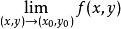
累次極限與重極限是兩個不同的概念,它們的存在性沒有必然的蘊含關係。下面兩個例子將說明這一點。
例1
設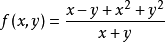 ,它關於原點的兩個累次極限分別為
,它關於原點的兩個累次極限分別為
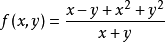



例2
設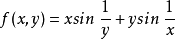 ,它關於原點的兩個累次極限都不存在。這是因為對任何
,它關於原點的兩個累次極限都不存在。這是因為對任何 ,當
,當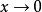 時
時 的第二項不存在極限。同理,對任何
的第二項不存在極限。同理,對任何 ,當
,當 時
時 的第一項也不存在極限。但是由於
的第一項也不存在極限。但是由於
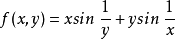

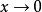







重極限與累次極限之間的聯繫
定理1
若 在點
在點 存在重極限
存在重極限




推論1
若累次極限


推論2
若累次極限
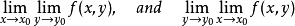
存在但不相等,則重極限

定理1保證了在重極限與一個累次極限都存在時,它們必相等,但它們對另一個累次極限的存在性卻得不出什麼結論。
