基本介紹
- 中文名:索菲熱爾曼質數
- 實際性:猜想
- 特徵:7位個位數
- 證明者:索菲·熱爾曼
- 又稱:索菲熱爾曼素數
定義
舉例
 1998 Hoffmann
1998 Hoffmann

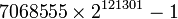 2005
2005特性
和梅森數的關係
出現頻率
 頻率公式
頻率公式
 1998 Hoffmann
1998 Hoffmann

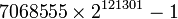 2005
2005 頻率公式
頻率公式索菲·熱爾曼出身巴黎一個殷實的商人家庭,從小熱愛數學,但不為家庭所鼓勵。身為女性,熱爾曼的故事顯出了當時女性求學的困難和自卑。她總不想別人知道她女性的身份,...
索菲·熱爾曼(1776~1831年)是法國的女數學家。她出身巴黎一個殷實的商人家庭,從小熱愛數學,但不為家庭所鼓勵。1831年,她因乳癌去逝。...
為索菲熱爾曼質數,即2*911+1=1823仍為質數 為三個連續質數和(293+307+311) 為艾森斯坦質數 高斯質數之一。 虧數,真因數和為1,虧度為910。 不尋常數...
第6個索菲熱爾曼素數:對應安全素數為59 第3個強素數 素數階乘素數。 第6個危險素數。前一個是19、下一個是31。 此數字雖然是自然素數,但不是高斯質數。前...
第3個索菲熱爾曼質數。 在十進制中,它是唯一一個以數字5為個位數的素數,其他以數字5為個位數的數均為5的倍數(注意10是5的倍數,因此對於任何整數n, 5|10n+5...
2003是2002與2004之間的自然數。也是年份。2003是奇數。2003是第304個質數。上一個質數為1999,下一個是2011。2003是第61個索菲熱爾曼質數。...
173(一百七十三)大寫:壹佰柒拾叄,是172與174之間的一個自然數,是一個質數。...質數。 艾森斯坦素數。 平衡質數(Balanced prime)。 索菲熱爾曼質數。 二個平方...
索菲熱爾曼質數 十進制下,既是可右截短質數,也是可左截短質數 此數字雖然是自然質數,但不是高斯質數。前一個有此性質的自然質數是41、下一個是61。(OEIS中...
第4個索菲熱爾曼素數 素數組合 (n,n+2,n+6,n+8) 之一(11,13,17,19);下一個組合為(101,103,107,109) 第2個唯一素數 [1] 高斯素數之一。 第...
第1個費馬素數((Fn=2的2n+1)) 第2個階乘素數( 2!+1)。前一個是2、下一個是5 第1個幸運素數 第2個索菲熱爾曼素數 第2個危險素數。前一個是2、...
索菲熱爾曼質數 此數字雖然是自然素數,但不是高斯素數。前一個有此性質的自然素數是109、下一個是137。(OEIS中的數列A002313) [1] 其第一象限之高斯質數的...
最小的能開始一個坎寧安鏈 (41, 83, 167) 的索菲熱爾曼素數 首六個素數之和,亦是3個連續素數之和:2+3+5+7+11+13=11+13+17=41 對於0≤n≤41的整...
第15個素數。前一個為43、下一個為53。 第五個安全素數:對應索菲熱爾曼素數為 23 陳素數 高斯質數之一。 第37個虧數,真因數和為1,虧度為46。前一個為...
回文質數第5個陳質數 第1個素數 第3個瓦格斯塔夫質數第3個森斯坦質數 第4個索菲熱爾曼質數若n=11,則n,n+2,n+6,n+8 (11, 13, 17, 19)均為素數。下...
第9個素數。前一個為19、下一個為29。 第5個階乘素數( 4!-1)。前一個是7、下一個是719。 陳素數 第4個安全素數:對應索菲熱爾曼素數為11 第5個索菲...
索菲熱爾曼素數 高斯質數之一。 第100個虧數,真約數和為1,虧度為130。前一個為130。 第90個不尋常數,大於平方根的素因數為131。前一個為130、下一個為133...
第1個費馬素數((Fn=2的2n+1)) 第2個階乘素數( 2!+1)。前一個是2、下一個是5 第1個幸運素數 第2個索菲熱爾曼素數 第2個危險素數。前一個是2、下一...
