索末菲橢圓軌道理論Sommerfeld's elliptical orbit theory,是德國物理學家A.索末菲在玻爾氫原子理論基礎上發展的理論,建於1916年。
基本介紹
- 中文名:索末菲橢圓軌道理論
- 外文名:Sommerfeld's elliptical orbit theory
- 提出者:A.索末菲
- 提出時間:1916年
簡介
計算方法
 (圖1)
(圖1) (圖2)
(圖2) (圖3)
(圖3) (圖4)
(圖4)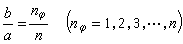 (圖5)
(圖5) (圖6)
(圖6)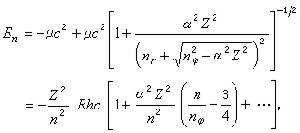 (圖7)
(圖7)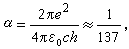 (圖8)
(圖8)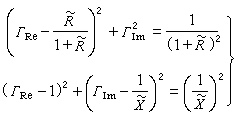 (圖10)
(圖10) (圖9)
(圖9)索末菲橢圓軌道理論Sommerfeld's elliptical orbit theory,是德國物理學家A.索末菲在玻爾氫原子理論基礎上發展的理論,建於1916年。
 (圖1)
(圖1) (圖2)
(圖2) (圖3)
(圖3) (圖4)
(圖4)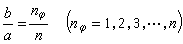 (圖5)
(圖5) (圖6)
(圖6)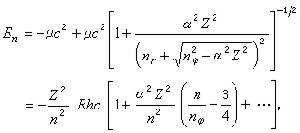 (圖7)
(圖7)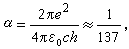 (圖8)
(圖8)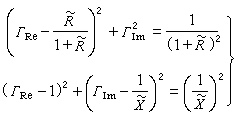 (圖10)
(圖10) (圖9)
(圖9)索末菲橢圓軌道理論Sommerfeld's elliptical orbit theory,是德國物理學家A.索末菲在玻爾氫原子理論基礎上發展的理論,建於1916年。...
阿諾德·索末菲(1868年12月5日~1951年4月26日)生於東普魯士的柯尼斯堡,卒...1916年,他對玻爾的理論提出修正,即引入了電子的橢圓軌道,在作這樣的修正時,他...
索末菲數是電子在第一玻爾軌道上的運動速度和真空中光速的比值。...... 地解釋了氫原子光譜和重元素 X 射線譜的精細結構以及正常塞曼效應(見索末菲橢圓軌道理論)...
原子理論(英語:Atomic theory)是物理學與化學中有關物質本質的科學理論。與物質...1916年,阿諾·索末菲將玻爾模型中電子的圓軌道推廣為橢圓軌道來解釋氫光譜新...
索末菲,A.德國理論物理學家。1868年12月5日生於東普魯士的柯尼斯堡(今蘇聯加里寧格勒)。1886年入柯尼斯堡大學主修數學,1891年得博士學位。1893~1894年在格丁...
前述關於氫原子的半經典理論稱為索末菲模型。其軌道是各種不同尺寸的橢圓軌道處於離散的傾斜平面。索末菲模型預測,原子沿著某直軸的磁矩,只能給出離散值。這預測...
2.玻爾原子結構的量子理論 3.玻爾理論的推廣 (1)皮克林線系的實質 (2)莫塞萊定律 (3)索末菲的橢圓軌道理論 (4)對應原理 (七)量子力學理論的建立 1.德布羅...
1915年,德國物理學家索末菲(Arnold Sommerfeld,1868-1951)把玻爾的原子理論推廣到包括橢圓軌道,並考慮了電子的質量隨其速度而變化的狹義相對論效應,導出光譜的精細...
玻爾的理論大大擴展了量子論的影響,加速了量子論的發展。1915年,德國物理學家索末菲(Arnold Sommerfeld,1868-1951)把玻爾的原子理論推廣到包括橢圓軌道,並考慮了...
玻爾的理論大大擴展了量子論的影響,加速了量子論的發展。1915年,德國物理學家索末菲(Arnold Sommerfeld,1868-1951)把玻爾的原子理論推廣到包括橢圓軌道,並考慮了...
早在玻爾理論之前,用分辨本領更高的儀器還發現氫原子主線系的譜線不是單線,而是有雙線的精細結構.後來索末菲(Sommerfeld)把玻爾理論推廣到橢圓軌道,得出表示類氫...
第一章原子軌道理論 第一節盧瑟福原子模型 第二節原子光譜規律 第三節玻爾的氫原子理論 第四節索末菲的橢圓軌道理論 第五節玻爾理論的局限性 第二章...
不考慮自轉時質量分布均勻球體的重力加速度求解方法的理論推導 如何在物理課堂上...索末菲橢圓軌道的簡單處理 《互感和自感》實驗教學設計 對一種斷電自感實驗失...
