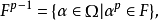純不可分擴張

純不可分擴張(purely inseparable extension )是一種重要的代數擴張。設K/F是代數擴張，若K中每個元均為F上的不可分元，則稱這個擴張為純不可分擴張。

基本介紹

• 中文名：純不可分擴張
• 外文名：purely inseparable extension
• 領域：數學
• 性質：代數擴張
• 元：不可分元
• 對偶概念：可分擴張

概念

純不可分擴張(purely inseparable extension )是一種重要的代數擴張。設K/F是代數擴張，若K中每個元均為F上的不可分元，則稱這個擴張為純不可分擴張。域的代數擴張K/F是純不可分的充分必要條件為F在K中的可分閉包就是F。特別地，當F的特徵為0時，K/F是純不可分的，若且唯若K=F；當F的特徵≠0時，K/F為純不可分的，若且唯若F共軛映射的個數l(K/F)=1。對於代數擴張K/F，若F在K中的可分閉包為S，則K/S為純不可分擴張，而S/F為可分擴張。擴張次數[K∶S]，[S∶F]分別稱為K在F上的不可分次數與可分次數，記為[K∶F]_i，[K∶F]_s。純不可分擴張具有傳遞性。當K/F是有限擴張時 ，

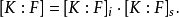
代數擴張

一類重要的域擴張。設E是F的擴域，若E中元皆為F上的代數元，則稱此域擴張為代數擴張，E稱為F的代數擴域，否則稱為超越擴張，而E稱為F的超越擴域。代數擴張具有傳遞性。當α是F上代數元時，其單代數擴域F(α)同構於F[x]/(p(x))，p(x)是α的最小多項式，(p(x))表F[x]中由p(x)生成的主理想。

對於一個數域P，如果ξ是域P上的一個不可約多項式在其擴域上的一個根，我們把ξ和域P的元素之間的和、差、積、商所組成的數集叫做域P上的一個代數擴張。

域的擴張

域論的基本概念之一。若域K包含域F作為它的子域，則稱K是F的一個擴張(或擴域)，F稱為基域，常記為K/F。此時，K可以看成F上的向量空間。研究擴域K(相對於基域F)的代數性質，是域論研究的一個基本內容。

若域E是F的擴域，K是E的擴域，則稱E是域擴張K/F的中間域。若K/F是域擴張，S是K的子集，且F(S)是K的含F與S的最小子域，稱F(S)為F添加S的擴域。當S={α₁，α₂，…，α_n}是有限集合時，F(α₁，α₂，…，α_n)稱為添加α₁，α₂，…，α_n於F的有限生成擴域(或者F上的有限生成擴張)。它由一切形如：

的元組成，其中α₁，α₂，…，α_n∈S，f，g是F上的n元多項式且：

由於這個原因，當F(α₁，α₂，…，α_n)關於F的超越次數≥1時，F(α₁，α₂，…，α_n)也稱為F上的代數函式域。當S={α}時，稱F(α)為F的單擴張域，也稱本原擴域。F的有限代數擴域K是單擴域的充分必要條件是，擴域K與基域間存在有限箇中間域。這是施泰尼茨(Steinitz，E.)證明的。

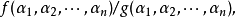
可分閉包

一種特殊的代數擴域。即域上最大的可分代數擴域。設K是F的代數擴域，K內所有F上的可分元組成的子域S稱為F在K內的可分閉包，它是F在K內可分擴域的最大者。若K是F的代數閉包，則稱F在K內的可分閉包為F的可分閉包，記為F_sep，它除F同構外是惟一的。利用可分閉包，可將一個代數擴張分為一個可分擴張和一個純不可分擴張來研究。

可分擴張

一種重要的域擴張。其特徵為p的域F的任意擴張K/F，Ω是K的代數閉包，若K與：

在F上是線性分離的，則稱K/F是可分擴張.當F是完備域時，F上任何擴張都是可分擴張。當K/F是代數擴張時，若α∈K在F上的最小多項式是可分多項式，則稱α是(F上的)可分代數元(簡稱F上可分元)。若K中每個元均為F上可分元，則稱K是F上可分擴張。若K/F有一個超越基S，使得K是可分的，則稱S是可分超越基。若K/F有這樣一個可分超越基，則稱此擴張K/F是可分生成的。完備域上的有限生成擴張均為可分生成擴張。可分擴張具有傳遞性。當K/F是有限生成，而且是可分擴張時，K/F是可分生成的。反之，可分生成的擴張必然是可分擴張。