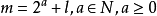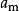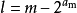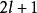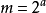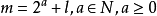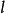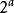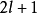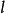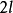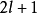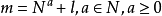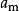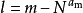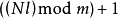約瑟夫問題

約瑟夫問題（有時也稱為約瑟夫斯置換，是一個出現在計算機科學和數學中的問題。在計算機編程的算法中，類似問題又稱為約瑟夫環。又稱“丟手絹問題”.）

基本介紹

• 中文名：約瑟夫問題
• 外文名：Josephus problem
• 別名：約瑟夫斯置換
• 類似問題：約瑟夫環
• 別稱：丟手絹問題

問題來歷

據說著名猶太歷史學家 Josephus有過以下的故事：在羅馬人占領喬塔帕特後，39 個猶太人與Josephus及他的朋友躲到一個洞中，39個猶太人決定寧願死也不要被敵人抓到，於是決定了一個自殺方式，41個人排成一個圓圈，由第1個人開始報數，每報數到第3人該人就必須自殺，然後再由下一個重新報數，直到所有人都自殺身亡為止。然而Josephus 和他的朋友並不想遵從。首先從一個人開始，越過k-2個人（因為第一個人已經被越過），並殺掉第k個人。接著，再越過k-1個人，並殺掉第k個人。這個過程沿著圓圈一直進行，直到最終只剩下一個人留下，這個人就可以繼續活著。問題是，給定了和，一開始要站在什麼地方才能避免被處決？Josephus要他的朋友先假裝遵從，他將朋友與自己安排在第16個與第31個位置，於是逃過了這場死亡遊戲。

17世紀的法國數學家加斯帕在《數目的遊戲問題》中講了這樣一個故事：15個教徒和15 個非教徒在深海上遇險，必須將一半的人投入海中，其餘的人才能幸免於難，於是想了一個辦法：30個人圍成一圓圈，從第一個人開始依次報數，每數到第九個人就將他扔入大海，如此循環進行直到僅餘15個人為止。問怎樣排法，才能使每次投入大海的都是非教徒。

問題分析與算法設計

約瑟夫問題並不難，但求解的方法很多；題目的變化形式也很多。這裡給出一種實現方法。

題目中30個人圍成一圈，因而啟發我們用一個循環的鏈來表示，可以使用結構數組來構成一個循環鏈。結構中有兩個成員，其一為指向下一個人的指針，以構成環形的鏈；其二為該人是否被扔下海的標記，為1表示還在船上。從第一個人開始對還未扔下海的人進行計數，每數到9時，將結構中的標記改為0，表示該人已被扔下海了。這樣循環計數直到有15個人被扔下海為止。

一般形式

約瑟夫問題是個有名的問題：N個人圍成一圈，從第一個開始報數，第M個將被殺掉，最後剩下一個，其餘人都將被殺掉。例如N=6，M=5，被殺掉的順序是：5，4，6，2，3，1。

分析：

（1）由於對於每個人只有死和活兩種狀態，因此可以用布爾型數組標記每個人的狀態，可用true表示死，false表示活。

（2）開始時每個人都是活的，所以數組初值全部賦為false。

（3）模擬殺人過程，直到所有人都被殺死為止。

pascal代碼1

　

var   a:array [1..20] of integer;  n,m,i,j,k,n1,m1:integer;beginreadln(m,n);for i:=1 to m do  a[i]:=i;m1:=m;n1:=1;while m1>0 dobegin  j:=(n+n1-1-1) mod m1 +1;  n1:=j;  m1:=m1-1;  writeln(a[j]);  for k:=j to m1 do    a[k]:=a[k+1];end;end.

C++代碼：

#include<iostream>using namespace std;main(){    bool a[101]={0};    int n,m,i,f=0,t=0,s=0;    cin>>n>>m;    do    {        ++t;//逐個枚舉圈中的所有位置        if(t>n)            t=1;//數組模擬環狀，最後一個與第一個相連        if(!a[t])            s++;//第t個位置上有人則報數        if(s==m)//當前報的數是m        {            s=0;//計數器清零            cout<<t<<' ';//輸出被殺人編號            a[t]=1;//此處人已死，設定為空            f++;//死亡人數+1        }    }while(f!=n);//直到所有人都被殺死為止}

無論是用鍊表實現還是用數組實現都有一個共同點：要模擬整個遊戲過程，不僅程式寫起來比較煩，而且時間複雜度高達O(nm），當n，m非常大（例如上百萬，上千萬）的時候，幾乎是沒有辦法在短時間內出結果的。我們注意到原問題僅僅是要求出最後的勝利者的序號，而不是要讀者模擬整個過程。因此如果要追求效率，就要打破常規，實施一點數學策略。

為了討論方便，先把問題稍微改變一下，並不影響原意：

問題描述：n個人（編號0~(n-1）），從0開始報數，報到（m-1）的退出，剩下的人繼續從0開始報數。求勝利者的編號。

我們知道第一個人（編號一定是（m-1）) 出列之後，剩下的n-1個人組成了一個新的約瑟夫環（以編號為k=m mod n的人開始）：

k k+1 k+2 ... n-2,n-1,0,1,2,... k-2

並且從k開始報0。

我們把他們的編號做一下轉換：

k --> 0

k+1 --> 1

k+2 --> 2

...

...

k-2 --> n-2

變換後就完完全全成為了（n-1）個人報數的子問題，假如我們知道這個子問題的解：例如x是最終的勝利者，那么根據上面這個表把這個x變回去不剛好就是n個人情況的解嗎？！！變回去的公式很簡單，相信大家都可以推出來：x'=(x+k) mod n

如何知道（n-1）個人報數的問題的解？對，只要知道（n-2）個人的解就行了。（n-2）個人的解呢？當然是先求（n-3）的情況 ---- 這顯然就是一個倒推問題！好了，思路出來了，下面寫遞推公式：

令f表示i個人玩遊戲報m退出最後勝利者的編號，最後的結果自然是f[n]

遞推公式

f[1]=0;

f[i]=(f[i-1]+m) mod i; (i>1）

有了這個公式，我們要做的就是從1-n順序算出f的數值，最後結果是f[n]。因為實際生活中編號總是從1開始，我們輸出f[n]+1

由於是逐級遞推，不需要保存每個f，程式也是異常簡單：

pascal代碼2

var  n,m,i,s,p:integer;  a:array[1..10000] of integer;begin  read(n,m);//這步不用說了吧？  for i:=1 to n do    a[i]:=1;//先全部賦值1  p:=0;s:=0;//統計人數和報數字用的  repeat    for i:=1 to n do    begin    if a[i]=0    then   continue; //用於等會排除出圈者         s:=s+a[i];//不斷累加(報數字)     if s=m then//出圈者     begin      write(i,' ');列印出圈者;      a[i]:=0;//明白剛才continue的意思了吧      p:=p+1;//人數減少一個;      s:=0;//重頭報起.    end;                      end;  until p=n;//直到人數到了end.

pascal代碼3

Var  a:array[1..100] of integer;  n,m,i,j,p:integer;Begin  write('Input n,m:');  readln(n,m);  for i:=1 to n do    a[i]:=i;  p:=1;                     {p用於記錄報數的位置}  for i:=1 to n do    begin      j:=0;                  {j用於記錄報到的人數}      while j<m do        begin          if a[p]<>0 then j:=j+1;          if p=n then p:=1 else p:=p+1;  {處理邊界情況}        end;      if p<>1           then begin write(a[p-1],' ');a[p-1]:=0;end       {處理邊界情況}           else begin write(a[n],' ');a[n]:=0;end;    end;end.

pascal代碼4

Var  a:array[1..100] of integer;  n,m,p,i,j:integer;Begin  readln(n,m);  for i:=1 to n-1 do   a[i]:=i+1;  a[n]:=1;  p:=n;  for i:=1 to n do    begin      for j:=1 to m-1 do         p:=a[p];      write(a[p],' ');      a[p]:=a[a[p]];   end;End.

c++

#include <iostream>using namespace std;const int m = 3;int main(){    int n, f = 0;    cin >> n;    for (int i = 1; i <= n; i++) f = (f + m) % i;    cout << f + 1 << endl;}

pascal代碼5

var n,m,i,s:integer;beginwrite('N M =');read(n,m);for i:=2 to n dos:=(s+m) mod i;writeln('The winner is ',s+1）;end.

這個算法的時間複雜度為O(n），相對於模擬算法已經有了很大的提高。算n，m等於一百萬，一千萬的情況不是問題了。可見，適當地運用數學策略，不僅可以讓編程變得簡單，而且往往會成倍地提高算法執行效率。

python代碼

該程式基於python3.x實現

#控制參數：nums = 41call = 3#參數定義：peoples = []for _ in range(nums):    peoples.append(True)result = []num =1#主邏輯while(any(peoples)):    for index,people in enumerate(peoples):        if people:            if num == call:                peoples[index] = False                result.append(index+1)#                print(index+1)#每輪的出局者                #                print(peoples)#每次的佇列狀態                num = 1                           else:                num += 1print('-'* 25)print('\n總數為%d,報數為%d' % (nums,call))        print('約瑟夫序列為：\n%s\n' % result)      print('-'* 25)

約瑟夫問題10e100版（from vijios)

描述 Description

n個人排成一圈。從某個人開始，按順時針方向依次編號。從編號為1的人開始順時針“一二一”報數，報到2的人退出圈子。這樣不斷循環下去，圈子裡的人將不斷減少。由於人的個數是有限的，因此最終會剩下一個人。試問最後剩下的人最開始的編號。

輸入格式 Input Format

一個正整數n，表示人的個數。輸入數據保證數字n不超過100位。

輸出格式 Output Format

一個正整數。它表示經過“一二一”報數後最後剩下的人的編號。

樣例輸入 Sample Input

9

樣例輸出 Sample Output

3

時間限制 Time Limitation

各個測試點1s

注釋 Hint

樣例說明

當n=9時，退出圈子的人的編號依次為：

2 4 6 8 1 5 9 7

最後剩下的人編號為3

初見這道題，可能會想到模擬。可是數據實在太大啦！！

我們先拿手來算，可知n分別為1，2，3，4，5，6，7，8...時的結果是1，1，3，1，3，5，7，1...

有如下規律：從1到下一個1為一組，每一組中都是從1開始遞增的奇數，且每組元素的個數分別為1，2，4...

這樣就好弄了！！

大體思路如下：

①read(a)

②b:=1,c:=1{b為某一組的元素個數，c為累計所加到的數}

③while c<a do (b:=b*2,c:=b+c){超過目標時停止加數}

⑥c:=c-b{退到前一組}

⑦x:=a-c{算出目標為所在組的第幾個元素}

⑧ans:=x*2-1{求出該元素}

⑨write(ans)

有了思路，再加上高精度就可以了。我寫的代碼比較猥瑣，因為是先把上面的思路敲進去，再寫過程，又把一些簡單的過程合到主程式中了，所以有點亂，也有點猥瑣。起提供思路的作用還是完全可以的吧~~~

var  a,b,c:array[1..105]of longint;  la,lb,lc,i:longint;  s:string;procedure incc;var  i:integer;begin  for i:=1 to 105 do    c:=c+b;  for i:=1 to 104 do    if c>9 then             begin               c:=c+cdiv10;               c:=c mod 10;             end;end;functioncxiaoa:boolean;vari:integer;begincxiaoa:=false;fori:=105downto1doifc<athenbegincxiaoa:=true;break;endelseifc>athenbreak;end;proceduredoubleb;vari:integer;beginfori:=1to105dob:=b*2;fori:=1to104doifb>9thenbeginb:=b+bdiv10;b:=bmod10;end;end;proceduredecc;vari,j:integer;beginfori:=1to104doifc>=bthenc:=c-belsebeginj:=i+1;whilec[j]=0doinc(j);whilej>idobeginc[j]:=c[j]-1;c[j-1]:=c[j-1]+10;dec(j);end;c:=c-b;end;end;procedurefua;vari:integer;beginfori:=1to104doifa>cthena:=a-celsebegina:=a-1;a:=a+10;a:=a-c;end;end;procedureoutit;vari,j:integer;beginfori:=1to105doa:=a*2;fori:=1to104doifa>9thenbegina:=a+adiv10;a:=amod10;end;ifa[1]>0thena[1]:=a[1]-1elsebeginj:=2;whilea[j]=0doinc(j);whilej>1dobegina[j]:=a[j]-1;a[j-1]:=a[j-1]+10;dec(j);end;a[1]:=a[1]-1;end;fori:=105downto1doifa>0thenbeginj:=i;break;end;fori:=jdownto1dowrite(a);end;beginreadln(s);la:=length(s);fori:=ladownto1doa:=ord(s[la+1-i])-ord('0');b[1]:=1;c[1]:=1;whilecxiaoadobegindoubleb;incc;end;decc;fua;outit;end.

猴子選王

問題表述

一． 問題描述：

一堆猴子都有編號，編號是1，2，3 ...m，這群猴子（m個）按照1-m的順序圍坐一圈，從第1開始數，每數到第N個，該猴子就要離開此圈，這樣依次下來，直到圈中只剩下最後一隻猴子，則該猴子為大王。

約瑟夫

"密碼問題"

問題描述：編號為1、2、3、...、N的N個人按順時針方向圍坐一圈，每人持有一個密碼（正整數）。從指定

編號為1的人開始，按順時針方向自1開始順序報數，報到指定數M時停止報數，報M的人出列，並將

他的密碼作為新的M值，從他在順時針方向的下一個人開始，重新從1報數，依此類推，直至所有的

人全部出列為止。請設計一個程式求出出列的順序，其中N≤30，M及密碼值從鍵盤輸入。

二． 基本要求：

（1） 輸入數據：輸入m,n m,n 為整數，n<m

（2）中文提示按照m個猴子，數n 個數的方法，輸出為大王的猴子是幾號 ，建立一個函式來實現此功能

編程解決

• 1.C程式
  

#include <stdio.h>#include <malloc.h>#defineLENsizeof(structmonkey)//定義structmonkey這個類型的長度struct monkey{int num;struct monkey *next;};struct monkey *create(int m){struct monkey *head,*p1,*p2;inti;p1=p2=(struct monkey*)malloc(LEN);head=p1;head->num=1;for(i=1,p1->num=1;i<m;i++){p1=(struct monkey*)malloc(LEN);p1->num=i+1;p2->next=p1;p2=p1;}p2->next=head;return head;}struct monkey *findout(struct monkey *start,int n){int i;struct monkey *p;i=n;p=start;for(i=1;i<n-1;i++)p=p->next;return p;}struct monkey *letout(struct monkey *last){struct monkey *out,*next;out=last->next;last->next=out->next;next=out->next;free(out);return next;}int main(){int m,n,i,king;struct monkey *p1,*p2;printf("請輸入猴子的個數m:\n");scanf("%d",&m);printf("每次數猴子的個數n:\n");scanf("%d",&n);if(n==1）{king=m;}else{p1=p2=create(m);for(i=1;i<m;i++){p2=findout(p1,n);p1=p2;p2=letout(p1）;p1=p2;}king=p2->num;free(p2）;}printf("猴王的編號是：%d\n",king);return 0;}

• C語言程式2
  

//猴子選大王問題（約瑟夫環問題）　#include<stdio.h>　#include<string.h>　#include<stdlib.h>　intfre(charmok[],intk)　{　inti;　printf("\n猴子編號：\n");　for(i=0;mok[i]!='\0';i++)　printf("%d\t",mok[i]);//輸出為踢出之前的編號，測試用　for(i=k;mok[i]!='\0';i++)　{　mok[i]=mok[i+1];　}//一個循環，將k以後的元素前移　putchar('\n');　for(i=0;mok[i]!='\0';i++)　printf("%d\t",mok[i]);//輸出踢出之後的編號，測試用　printf("\n按回車繼續下一輪:\n");　getch();//暫停，測試用　return0;　}　int main()　{　char mok[50];　int i;　int n,s,b;//n表示猴子總數；s表示步進；b表示元素個數及大王編號　int j,k;//j,k都是計數器　mok[0]=1;//初始化mok[0],讓後面編號更簡單的進行　printf("請輸入猴子的總數：\n");　scanf("%d",&n);//輸入猴子的總數　for(i=1;i<n;i++)　{　mok[i]=i+1;　}//對猴子進行編號　mok[n]='\0';//用0來表示數組的結尾　printf("請輸入循環單位：\n");　scanf("%d",&s);//單位長度　b=n;//統計猴子的個數　for(j=1,k=0;;j++,k++)　{　if(b==1)　{　b=mok[0];　break;　}//如果元素只剩下一個，那么退出循環　if(j==s)　{　printf("\n它出列了：%d\n",mok[k]);　fre(mok,k);//用於元素前移的函式　b--;　j=1;　}//將猴子從數組中踢出，並重置計數器J。　if(mok[k+1]=='\0')　k=-1;//重置計數器k，因為後面有k++所以k要在重置基礎上-1.　}//判斷是否為數組最後元素，重置計數器k。　printf("\n最終大王是他：%d\n",b);　return0;　}

• C語言程式3: 用數組模擬鍊表
  

#include<stdio.h>#include<malloc.h>int main(){int *person,i,node,n,m;scanf("%d%d",&n,&m);person=(int*)malloc(sizeof(int)*(n+1));for(i=1;i<n;i++)//初始化圈{person[i]=i+1;//i表示編號為i的人,person[i]的值表示編號為i的人的下一個人的編號}person[n]=1;//編號為n的下一個人的編號是1node=1;while(node!=person[node])//如果某個人的下一個人不是自己,意味著人數超過1人{for(i=1;i<m-1;i++)//這個循環終止於被殺的人的前一個人{node=person[node];//下一個人的編號為node,node的值來自於前一個人的person[node]}printf("%d",person[node]);//輸出被殺的人編號person[node]=person[person[node]];//修改被殺的人的前一個人的person[node]為被殺的人的後一個人的編號node=person[node];//這句話中的node是被殺的人後一個人}printf("%d",node);//輸出最後倖存者的編號return 0;}

• pascal程式：
  

vara:array[1..10000]ofinteger;n,s,i,j:integer;beginread(m,n);fori:=1tomdoa[i]:=1;j:=0;fori:=1tomdobegins:=0;whiles<ndobeginifj<mtheninc(j)elsej:=1;s:=s+a[j];end;write(j);a[j]:=0;end;end.

• c++程式
  

#include<iostream>#include<conio.h>using namespace std;main(){    int n,m,i,s=0;    cout<<"N：";cin>>n;       cout<<"M：";cin>>m;    for(i=2;i<=n;i++)    s=(s+m)%i;    cout<<"新的大王是："<<s+1;    getch();  }

• 約瑟夫數學算法
  

#include<stdio.h>#include<conio.h>intmain(void){intn,i=0,m,p;scanf("%d%d",&n,&m);//n總人數，m步長while(++i<=n){p=i*m;while(p>n)p=p-n+(p-n-1）/(m-1）;printf("%d\n",p);}getch();return0;}

• 約瑟夫遞推算法
  

#include<iostream>usingnamespacestd;intking(intM,intN){intk=0;for(inti=2;i<=M;i++)k=(k+N)%i;return++k;}intmain(){intn,m;while(scanf("%d%d",&n,&m)&&n&&m){cout<<king(n,m)<<endl;}return0;}

• 2、PHP模擬算法
  

php有非常完善的數據結構模擬方案,可以非常簡潔的解決這樣的問題!

functionking($n,$m){$monkey=range(1,$n);//模擬建立一個連續數組$i=0;while(count($monkey)>1){$i+=1;//開始查數$head=array_shift($monkey);//直接一個一個出列最前面的猴子if($i%$m!=0){array_push($monkey,$head);//如果沒數到m或m的倍數,則把該猴放回尾部去.}//否則就拋棄掉了}return$monkey[0];}echo'剩餘',king(3,4),'號猴子';

3. Python遍歷數組

def Monkey(n, M):    if n == 0 or M == 1: #過濾兩種特殊情況        return 0    L = list(map(list,list(enumerate([True] * n,start=1)))) #兩種狀態以布爾值表示    counter = 0    while [L[i][1] for i in range(len(L))].count(True) > 1:        for i in range(len(L)):            if L[i][1] == True:                counter += 1            if counter % M == 0 and L[i][1] == True:                L[i][1] = False    return list(filter(lambda x:x[1] == True, L))[0][0]    Monkey(2009, 3)

筆算解決

筆算解決約瑟夫問題

在M比較小的時候 ，可以用筆算的方法求解，

M=2

即N個人圍成一圈，1，2，1，2的報數，報到2就去死，直到只剩下一個人為止。

當N=2^k的時候，第一個報數的人就是最後一個死的，

對於任意的自然數N 都可以表示為N=2^k+t，其中t<n/2

於是當有t個人去死的時候，就只剩下2^k個人 ，這2^k個人中第一個報數的就是最後去死的。這2^k個人中第一個報數的人就是2t+1

於是就求出了當M=2時約瑟夫問題的解：

求出不大於N的最大的2的整數次冪，記為2^k，最後一個去死的人是2(N-2^k)+1

M=3

即N個人圍成一圈，1，2，3，1，2，3的報數，報到3就去死，直到只剩下一個人為止。

此時要比M=2時要複雜的多

我們以N=2009為例計算

N=2009，M=3時最後被殺死的人記為F（2009,3），或者可以簡單的記為F（2009）

假設這種情況下還剩下n個人，則下一輪將殺死[n/3]個人，[]表示小於等於這個數的最大整數，還剩下n-[n/3]個人

設這n個人為a1,a2,...,a(n-1）,an

從a1開始報數，一圈之後，剩下的人為a1,a2,a4,a5,...a(n-n mod 3-1）,a(n-n mod 3+1）,..,an

於是可得：

1、這一輪中最後一個死的是a(n-n mod 3），下一輪第一個報數的是a(n-n mod 3+1）

2、若3|n，則最後死的人為新一輪的第F(n-[n/3]）個人

若n mod 3≠0 且f(n-[n/3])<=n mod 3則最後死的人為新一輪的第n-[n/3]+F(n-[n/3])-（n mod 3）人

若n mod 3≠0 且f(n-[n/3])>n mod 3則最後死的人為新一輪的第F(n-[n/3])-（n mod 3）人

3、新一輪第k個人對應原來的第 3*[(k-1）/2]+(k-1）mod 2+1個人

綜合1，2，3可得：

F（1）=1,F（2）=2,F（3）=2,F（4）=1,F（5）=4，F（6）=1，

當f(n-[n/3])<=n mod 3時 k=n-[n/3]+F(n-[n/3])-（n mod 3），F(n)=3*[(k-1）/2]+(k-1）mod 2+1

當f(n-[n/3])>n mod 3時 k=F(n-[n/3])-（n mod 3） ，F(n)=3*[(k-1）/2]+(k-1）mod 2+1

這種算法需要計算 [log（3/2）2009]次 這個數不大於22，可以用筆算了

於是：

第一圈，將殺死669個人，這一圈最後一個被殺死的人是2007，還剩下1340個人，

第二圈，殺死446人，還剩下894人

第三圈，殺死298人，還剩下596人

第四圈，殺死198人，還剩下398人

第五圈，殺死132人，還剩下266人

第六圈，殺死88人，還剩下178人

第七圈，殺死59人，還剩下119人

第八圈，殺死39人，還剩下80人

第九圈，殺死26人，還剩下54人

第十圈，殺死18人，還剩36人

十一圈，殺死12人，還剩24人

十二圈，殺死8人，還剩16人

十三圈，殺死5人，還剩11人

十四圈，殺死3人，還剩8人

十五圈，殺死2人，還剩6人

F（1）=1,F（2）=2,F（3）=2,F（4）=1,F（5）=4，F（6）=1，

然後逆推回去

F（8）=7 F（11）=7 F（16）=8 f（24）=11 f（36）=16 f（54）=23 f（80）=31 f（119）=43 f（178）=62 f（266）=89 f（398）=130

F（596）=191 F（894）=286 F（1340）=425 F（2009）=634

規律解決

視頻中給出了經典的約瑟父問題的數學解法，當猴子選王問題的N=2時就是經典的約瑟父問題

對於經典約瑟父問題，視頻中的解法是：

1）找出令等式 成立的最大的 ，記為

2）求解出

3）所以，最後留下來的人的序號為

視頻中給出的解釋是：

當 時，序號為1的人總是是最後留下來的人。對於 ，當去掉 個人後，剩下的人正好組成 個人圍成的圈，此圈中的序號1的人將是最後留下來的人。而對應到原來的圈，這個人的序號就是 ，因為去掉 個人時正好就跳過了 個人，而下一個人的序號就是 。

推廣到猴子選王問題，從以上解法不難看出，解法就是把2換成N，即：

1）找出令等式 成立的最大的 ，記為

2）求解出

3）所以，最後留下來的猴子的序號為 ，mod是取餘數，例如：3 mod 2 = 1

--------------------------

m=8, N=3，8=3^1+5, 按照他的算法，此時N=3，l=5, 按照他的算法最後剩下來的是8,事實上很容易直接驗算最後留下來的是7，上面的公式是錯誤的。