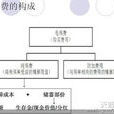
基本介紹
- 中文名:精算等價原理
- 所屬領域:保險
- 套用:純保費
- 屬性:保險理論
基本概念,公式解釋,文字解釋,
基本概念
首先你要理解這兩個概念:精算現值與精算等價原理。
保險實務中,純保費與理賠額的發生通常不會在同一個時間點上,應該將兩者放在同一個時間點上進行比較。一般將純保費與理賠額折現到保單(policy)生效這個點上。這樣,對純保費和理賠額的比較就不能單純的看其數額的大小,還要看資金的時間價值,保險標的物的死亡時間。為了解決這個問題,於是我們引入精算現值。精算現值與通常的資金現值的不同之處在於前者考慮了標的物死亡機率。收入(純保費)與支出(理賠額)在保單生效時的精算現值相等就是所謂的“精算等價原理”,純保費就是運用精算等價原理來計算的。
公式解釋
我以保險精算等價來對這個做出解釋吧,比如:
PR[T(20)>50]=0.70等價於50P20=0.7
PR[T(20)≤30]=0.11推出PR[T(20)>30]=0.89等價於30P20=0.89
而有個公式是:
(T+U)PX=TPX*UP(X+T) 括弧裡面的也都是下標數字
推出:50P20=30P20*20P50
於是20P50=50P20/30P20=0.7/0.89=0.7865
文字解釋
文字來解釋的話
這個題是這個意思:
已知一個20歲的人還能再活50年(即活到70歲)的機率是0.7
還已知一個20歲的人不能再多活30年的機率是0.11(也就是說一個20歲的人還能活到50歲的機率是0.89)
問:一個50歲的人還能多活20年(即活到70歲)的機率是多少?
而答案里的20P50=50P20/30P20就是說
一個50歲的人能活到70歲的機率=在已知“他(她)能從20歲活到50歲的機率”的條件下,他(她)能從20歲活到70歲的機率有多