簡介
粒子衰變是一
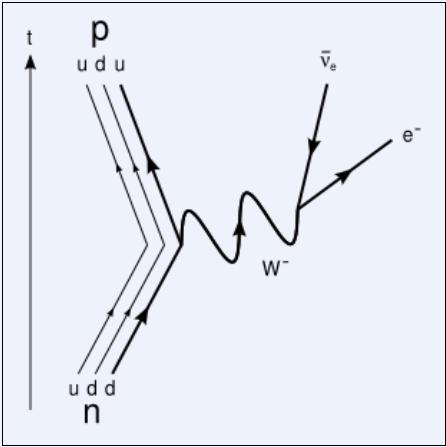
基本粒子變成其他基本粒子的自發過程。在這個過程中,一基本粒子變成質量更輕的另一種基本粒子,及一中間粒子,例如μ子衰變中的
W玻色子。這中間粒子隨即變成其他粒子。如果生成的粒子不穩定,那么衰變過程還會繼續。粒子衰變這種過程,與
放射性衰變不一樣,後者為一不穩定的
原子核,變成一更小的原子核,當中還伴隨著粒子或射線的發射。
粒子壽命列表
所有數值均來自粒子數據小組:
種類
| 名稱
| 符號
| 能量 (MeV)
| 平均壽命
|
輕子
| 電子 / 正電子
| e-/e+
| 0.511
| 年
|
μ子 / 反μ子
| μ-/μ+
| 105.6
| 秒
|
τ子 / 反τ子
| τ-/τ+
| 1777
| 秒
|
介子
| 中性π介子
| π0
| 135
| 秒
|
帶電π介子
| π+/π-
| 139.6
| 秒
|
重子
| 質子 / 反質子
| Ρ-/Ρ+
| 938.2
| > 1029年
|
中子 / 反中子
| n/ǹ
| 939.6
| 885.7 秒
|
玻色子
| W玻色子
| W+/W-
| 804,000
| 10 − 25 秒
|
W玻色子
| Z0
| 91000
| 10 − 25 秒
|
生還機率
把一個粒子的平均壽命標記為τ,這樣粒子在時間t後仍生還(即未衰變)的機率為P(t) = e-λtγ
衰變率
設一粒子質量為
M,則衰變率可用下面的通用公式表示其中
n為原衰變所生成的粒子數,m為連線始態與終態的不變矩陣上的元,dФn為相位空間的元,即為粒子
i的
四維動量。

四維動量
在狹義相對論中,四維動量是將古典三維動量推廣到四維空間。 動量是三維向量; 類似地,四維動量是時空中的四向量。 具有相對論能量E和三空間動量p =(px,py,pz)=γmv的粒子的逆向四維動量,其中v是粒子的三空間速度,γ是洛倫茲因子。
mv是粒子的平均非相對動量,m是其餘質量。四維動量在相對論計算中是有用的,因為它是洛倫茲矢量。 這意味著很容易跟蹤在
洛倫茲變換下如何變換。