簡單類型 lambda 演算是連線詞只有→(函式類型)的有類型 lambda 演算。這使它成為規範的、在很多方面是最簡單的有類型 lambda 演算的例子。
基本介紹
- 中文名:簡單類型λ演算
- 外文名:Simple Type lambda calculus
- 學科:數學
概念,類型,項,
概念
簡單類型lambda演算是連線詞只有→(函式類型)的有類型lambda演算。這使它成為規範的、在很多方面是最簡單的有類型lambda演算的例子。簡單類型也被用來稱呼對簡單類型 lambda 演算的擴展比如積、陪積或自然數(系統 T)甚至完全的遞歸(如PCF)。相反的,介入了多態類型(如系統F)或依賴類型(如邏輯框架)的系統不被當作是簡單類型。簡單類型 lambda 演算最初由阿隆佐·邱奇在 1940 年介入來嘗試避免無類型 lambda 演算的悖論性使用。
類型
簡單類型lambda演算的類型構造自基本類型(或類型變數)α,β,γ,…,給定類型σ,τ我們能構造σ→τ。邱奇只使用了兩個基本類型,o是命題的類型,ι是個體的類型。這種演算經常只有一個基本類型,通常考慮為o。
→是右結合的:我們讀σ→τ→ρ為σ→(τ→ρ)。對每個類型σ我們指派一個數字o(σ),它是σ的階。對於基本類型,我們設定o(α)=0,而對於函式類型我們遞歸的定義o(σ→τ)=max(o(σ)+1,o(τ))。
項
要定義有給定類型的lambda項的集合,我們介入定類型上下文Γ,Δ,…,它們是形如x:σ的類型假定的序列,這裡的x是變數。我們介入判斷Γ⊢t:σ,它意味著t在上下文Γ中是類型σ的項,它們由下列定類型規則給出:
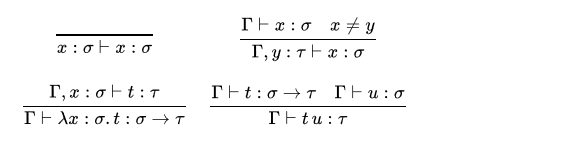
規則
換句話說,
1.如果 x 有類型 σ ,我們知道 x 有類型 σ。
2.在特定上下文中,如果 x 有類型 σ ,而我們有某個不是 x 的 y,則 y 有類型 τ 的事實,和上述上下文一起,允許我們推出 x 有類型 σ 。更加清楚的,向上下文增加一個新值不改變現存的值(假定新值不同於以前的值之一)。
3.在特定上下文中,如果 x 有類型 σ,而 t 有類型 τ ,則我們在同一個上下文中,可以構造lambda 抽象 λ x : σ . t ,它有類型 σ → τ 。
4.在特定上下文中,如果 t 有類型 σ → τ ,而 u 有類型 σ,則我們可以構造表達式 t u,它有類型 τ。這捕獲了函式套用的概念。