簡單指數不等式(simple exponential inequality)亦稱最簡指數不等式,是一種常見的指數不等式,即形如ax<b(a>0,a≠1),ax>b(a>0,a≠1)的不等式。
基本介紹
- 中文名:簡單指數不等式
- 外文名:simple exponential inequality
- 所屬學科:數學
- 別稱:最簡指數不等式
- 所屬問題:初等代數(不等式)
基本介紹,簡單指數不等式的解法,例題解析,
基本介紹
如果一個不等式里包含有底數是常數,指數出現未知數的項,這樣的不等式叫做指數不等式。
對於含有未知數字母的一些簡單的指數不等式,可以根據不等式的基本性質,並利用指數函式和對數函式的單調性求得其解,或是轉化為代數不等式再求解,至於稍複雜一些的指數不等式,是不可能用初等方法求解的。
簡單指數不等式的解法
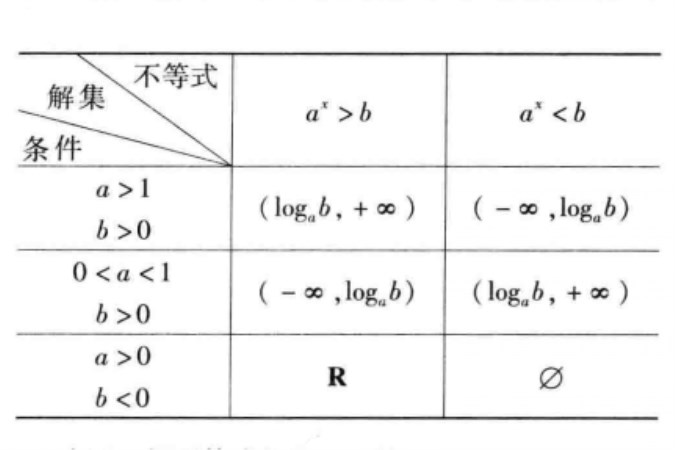
對於形如ax>b或ax<b(a>0且a≠1)的不等式,若b>0,則只需兩邊取對數,再利用對數函式的增減性來解。
1.解ax>b:
若b≤0,一切實數都是不等式的解;
若b>0,且當0<a<1時解為x<logab,當a>1時,解為x>logab。
2.解ax<b:
若b≤0,不等式無解;
若b>0,且當0<a<1時,解為x>logab,當a>1時,解為x<logab。
例題解析
【例1】解不等式 。
。

解: 原不等式變形為



【例2】解不等式

解 原不等式即為