簡單折線(simple broken line)是最常見的一種折線,滿足下列條件的折線稱為簡單折線: 1.對於任意兩邊,它們除頂點外無其他公共點; 2.頂點與邊上異於端點的任一點不重合;3.每一頂點至多是兩條邊的端點。
基本介紹
- 中文名:簡單折線
- 外文名:simple broken line
- 所屬學科:數學(幾何學)
- 屬性:最常見的一種折線
- 分類:凸折線,凹折線
定義
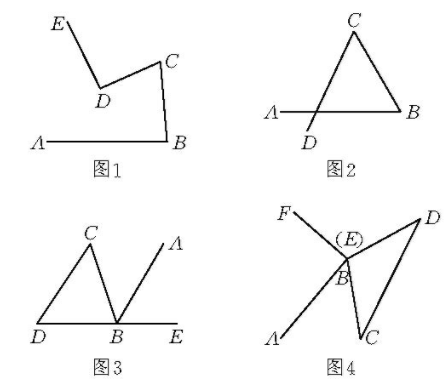
簡單折線的分類








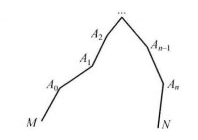
線性絕對值函式的圖形














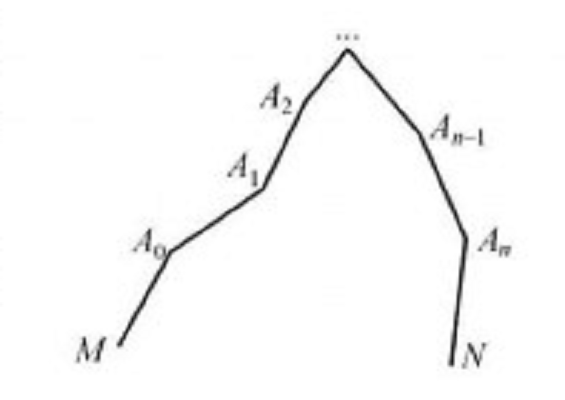
簡單折線(simple broken line)是最常見的一種折線,滿足下列條件的折線稱為簡單折線: 1.對於任意兩邊,它們除頂點外無其他公共點; 2.頂點與邊上異於端點的任一點不重合;3.每一頂點至多是兩條邊的端點。
























簡單折線(simple broken line)是最常見的一種折線,滿足下列條件的折線稱為簡單折線: 1.對於任意兩邊,它們除頂點外無其他公共點; 2.頂點與邊上異於端點的任一點不重合;3.每一頂點至多是兩條邊的端點。定...
平面上若干條線段順次首尾相接(每條最多同另外兩條聯結且端點不在另外線段內部)構成的圖形,稱為(平面)折線;如折線每邊都有兩鄰邊,就叫(封)閉折線,否則,叫開折線.這樣就可對摺線進行初步的分類和對幾個常用概念給予明確的界定:邊不相交的折線為簡單折線,簡單閉折線叫作多邊形。多邊形劃分平面為兩部分,有限...
簡單球面折線 簡單球面折線(simple spherical broken line)球面折線的一種。指滿足下述條件的球面折線:1.除頂點外,任意兩邊都沒有其他公共點.2.相鄰兩邊的公共端點以及折線的兩個端點都不在其他邊上.
折線圖是排列在工作表的列或行中的數據可以繪製到折線圖中。折線圖可以顯示隨時間(根據常用比例設定)而變化的連續數據,因此非常適用於顯示在相等時間間隔下數據的趨勢。在折線圖中,類別數據沿水平軸均勻分布,所有值數據沿垂直軸均勻分布。簡介 如果分類標籤是文本並且代表均勻分布的數值(如月、季度或財政年度),...
以簡單球面多邊形的兩個不相鄰的頂點為端點的大圓弧稱為該簡單球面多邊形的對角線。簡單球面折線 (simple spherical broken line)簡單球面折線是球面折線的一種,指滿足下述條件的球面折線:1、除頂點外,任意兩邊都沒有其他公共點;2、相鄰兩邊的公共端點以及折線的兩個端點都不在其他邊上。
組成折線的所有線段都在同一平面內的折線稱為平面折線,否則稱為空間折線。凡不相鄰的兩邊不相交的折線稱為簡單折線,把一條平面簡單折線的任一條邊向兩方延長成直線,如果能使這條折線的其他各邊都在這條直線的同側,那么這條平面折線稱為凸折線。連結非封閉折線的兩個端點的線段稱為折線的鎖線。空間折線與空間...
《認識折線統計圖》是如東縣於港國小提供的微課課程,主講教師是曹亞冬。課程簡介 在這個教學視頻片段中,主要通過教師的分析與講解,讓學生在具體的統計活動中,認識簡單的折線統計圖,了解折線統計圖的結構,體會折線統計圖的特點;能運用簡單的折線統計圖表示數據,感受統計是分析問題、解決問題的策略與方法。課中立足...
邊不相交的折線稱為簡單折線,簡單封閉折線稱為多邊形,多邊形將平面分為兩部分,其中有限部分稱為多邊形的內部,不難證明有:定理2 n邊形內部可用不相交的對角線劃分為n-2個三角形。定理3 n邊形內角和等於(n-2)π。沿折線一條邊經頂點A走向鄰邊,如向左(右)拐,A就叫作邊AB的左(右)折點(圖3(a)),稱...
簡單球面折線是球面折線的一種,指滿足下述條件的球面折線:1、除頂點外,任意兩邊都沒有其他公共點;2、相鄰兩邊的公共端點以及折線的兩個端點都不在其他邊上。凸球面折線 凸球面折線是一種簡單球面折線,即對摺任一邊所在大圓來說,其餘各邊都在同一半球內的簡單球面折線。不是凸球面折線的簡單球面稱為凹球面折線...
然後O1向弱側底角移動。注意,在CP3中,我們又回到O2在O5的掩護下折線切入基本的折線動作。傳切選擇 F 圖F描述了O2傳球給底角後一個簡單的傳切戰術,如果O2在切入後沒有接到傳球,然後所有的外圍球員在輪轉跑位去填補該區域。O5為O2切出底角做掩護。G 圖G描述了快速回傳(可能是給另一側後衛的長傳)和給在另...
《複式折線統計圖》是人教課標版國小數學第十冊第六單元統計(2)的內容,這一教學內容,其教材編排特點如下:(1)從解決問題的需要出發,引出複式折線統計圖,凸顯複式折線統計圖的作用與特點;(2)重視利用統計圖中的信息進行相應的分析、比較和簡單的判斷和推理;(3)恰當控制教學要求,避免不必要的製圖操作。B...
例如,由兩段有向線段組成的折線,第一段有向線段選取“↑”、“↗”、“→”等八個方向,第二段有向線段選取與第一有向線段0°、90°、180°、270°四種夾角的方向進行分類,理論上有8×4=32種不同組合的折線類型,可與26個英文字母及其它控制字元建立對應關係。主要用途 由於折線筆畫簡單,只需很小的觸摸...
簡單球面多邊形,球面多邊形的一種.指由封閉的簡單球面折線所圍成的球面多邊形.如果對於一個簡單球面多邊形的每一邊所在的大圓而言,其餘各邊都位於以該大圓為界的同一半球面內,則該簡單球面多邊形稱為凸球面多邊形;否則,稱為凹球面多邊形.對於凹球面多邊形可以通過添加適當大圓弧化為凸球面多邊形來研究.凸球面多邊形的...
“卷殺”是用作簡單折線求得近似拋物線的方法,主要用來保持外觀及構件上的弧線有共同變化規律。它的作圖方法是:把欲制弧線部分在縱、橫坐標上的高度、長度都均分為相同分數,並把諸段自外至內、自下至上編為1至n號;自橫坐標之1、2……至n-1諸點分別向縱坐標上的2、3……至n點連直線;諸線相交後連成...
sparkline是一類信息體積小和數據密度高的圖表。它被用作一些測量,相關的變化的信息呈現的方式,如平均溫度,股市交投活躍。sparkline常常以一組多條的形式出現 在柱狀圖,折線圖當中。sparkline的提出 sparkline最初是由Edward Tufte(愛德華塔夫特)提出的,具有數據豐富,結構簡單,圖表小巧的特點。在excel中,sparkline...
如果對於一個簡單球面多邊形的每一邊所在的大圓而言,其餘各邊都位於以該大圓為界的同一半球面內,則該簡單球面多邊形稱為凸球面多邊形;否則,稱為凹球面多邊形。簡介 簡單球面多邊形是球面多邊形的一種,指由封閉的簡單球面折線所圍成的球面多邊形。如果對於一個簡單球面多邊形的每一邊所在的大圓而言,其餘各邊都位於以...
統計圖是根據統計數字,用幾何圖形、事物形象和地圖等繪製的各種圖形。它具有直觀、形象、生動、具體等特點。統計圖可以使複雜的統計數字簡單化、通俗化、形象化,使人一目了然,便於理解和比較。因此,統計圖在統計資料整理與分析中占有重要地位,並得到廣泛套用。在解答資料分析測驗中有關統計圖的試題時,既要考察圖...
推移圖是用於觀察數據隨時間的變化的一種好方法,另外,影像數據的要因如能分別計入,就可以了解其影響度。推移圖非常簡單、一目了然。以不良率隨著時間的推移圖為例,每天將不良率在圖以點的形式標出,然後用直線將每一點連線起來,形成的折線就是不良推移率。製圖 製作步驟 推移圖製作步驟可以簡單概括為:(1)...
不自交的封閉折線可以出現兩個頂點相重合,一個頂點在另一條邊上及兩條邊有一部分(或全部)重合的特殊情形。因此,可以出現圖2(a)的六邊形ABCDEC、圖2(b)的五邊形和圖2(c)的四邊形。為排除以上情況,引進以下概念:由簡單閉折線所圍成的多邊形稱為簡單多邊形,其他多邊形稱為複雜多邊形。上面圖1是簡單多邊形,圖...
該圖像可以直接複製、貼上到Office 2000的其他程式中(比如Word、PowerPoint)使用,也可以製作成圖片檔案。最簡單的方法是把它複製/貼上到畫圖程式(Windows 9x/2000附屬檔案中)中存為BMP檔案,還可以通過圖片工具(比如ACDSee)轉換為JPG檔案,以減少占用的磁碟存儲空間。在Excel中你稍微留意一下,就可以注意到,一般的...
1.同類中的任意兩點,都能用一條與 F 無公共點的球面折線連結起來;2.不同類的任何兩點,不能用一條與 F 無公共點的球面折線連結起來。例如,球面大圓把球面分成的兩個半球面都是球面區域,兩個相交的大圓把球面分成四個區域。簡單球面多邊形的內部 (interior of a simplespherical polygon)球面幾何的基本概念...
3.5 簡單折線 第4章 三角形方程 4.1 軼聞一則 4.2 三角形方程的一般形式 4.3 三角形方程的特殊式 4.4 建立三角形方程的仿射變換法 4.5 關於三角形方程的套用 第5章 四邊形的方程 5.1 平行四邊形方程 5.2 一般四邊形方程(一)5.3 一般四邊形方程(二)5.4 一般四邊形方程(三)5.5 射影變換...
建立圖表的過程非常簡單,只要按照【圖表嚮導】的有關說明,一步一步地進行操作,即可完成圖表的製作。下面結合實例進行說明。(1)選取單元格區域A2:M3,單擊工具列上的【圖表嚮導】按鈕,或單擊【插入】選單,選擇【圖表】項,出現【圖表嚮導-4步驟之1-圖表類型】對話框,在【圖表類型】中選【折線圖】,在【...
組成多邊形的線段至少有3條,三角形是最簡單的多邊形。組成多邊形的每一條線段叫做多邊形的邊;相鄰的兩條線段的公共端點叫做多邊形的頂點;多邊形相鄰兩邊所組成的角叫做多邊形的內角;連線多邊形的兩個不相鄰頂點的線段叫做多邊形的對角線。多邊形內角的一邊與另一邊反向延長線所組成的角,叫做多邊形的外角。在多邊形的每...
