等變映射

在數學中，對於從一個具有對稱性的空間到另一個具有對稱性的空間（比如對稱空間（symmetric space））的函式，等變性（equivariance）指的是該函式的對稱性所具有的一種形式。當一個函式的定義域和陪域被同一個對稱群作用，且函式與群的作用交換時，我們稱該函式是一個等變映射（equivariant map）。也就是說，套用對稱變換然後計算函式所得到的結果，和計算函式然後套用變換得到的結果是一樣的。

等變映射推廣了不變數（invariant）的概念，即在對函式參數作對稱變換後，函式的值不變。等變映射的值通常（不嚴格地）稱為不變數。

在統計推斷中，數據統計變換下的等變性是各種估計方法的一個重要性質，詳見不變估計量（invariant estimator）。在純數學中，等變性是等變拓撲及其子課題等變上同調（equivariant cohomology）和等變穩定同倫論（equivariant stable homotopy theory）的中心研究對象。

基本介紹

• 中文名：等變映射
• 外文名：equivariant map
  G-map
• 所屬學科：群論
• 別名：G映射

定義

我們可以用群G的G集這個概念來將等變性形式化。這一數學對象是由一個數集和上的群G的一個作用組成。X與Y均為同一個群G的G集，如果

對所有與成立，那么稱為等變映射。

右作用

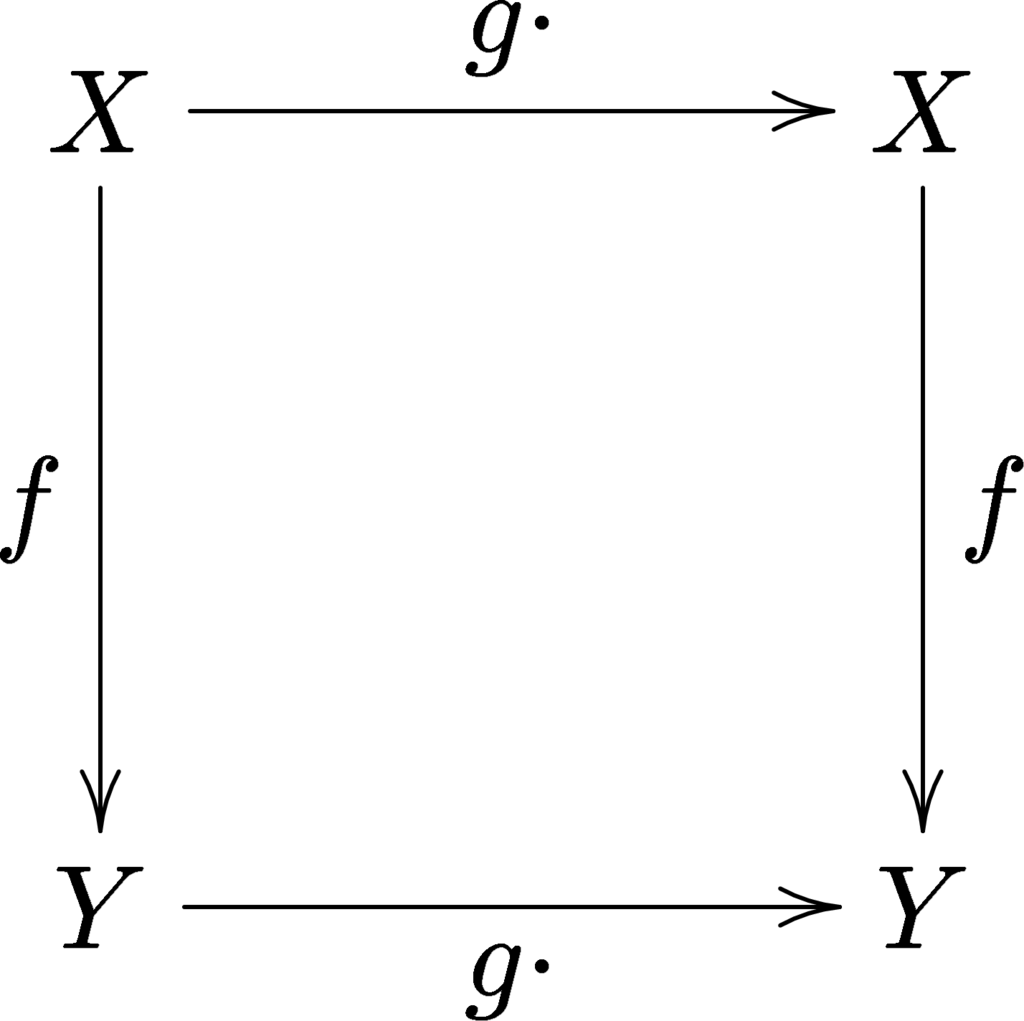
注意，如果其中一個或兩個作用是右作用，則等變條件必須適當修改成：

範疇論

等變映射是G集範疇（對於一個取定的G）中的同態。從而它們也稱為 G態射（G-morphism）、G映射（G-map）或 G同態（G-homomorphism）。G-集合的同構就是等變雙射（雙射的等變映射）。

等變條件也能理解為下面的交換圖表。注意，表示映射取元素得到。

交換圖表。

交結映射

對 G 的線性表示，由一個完全類似的定義。具體地說，如果 X 與 Y 是 G 的兩個線性表示的表示空間，如果它與 G 的作用交換，則一個線性映射 f : X → Y 稱為這個表示的一個交結映射（intertwining map）或交結子（intertwiner）。從而一個交結運算元是兩個線性表示/作用時等變映射的特例。

或者，G 在域 K 上表示的交結映射與 K[G]-模的一個模同態是同一個東西，這裡 K[G]是 G 的群環。

在某些情形，如果 X 與 Y 都是不可約表示，則一個交結映射（若不是零映射）只有兩個表示等價（即作為模是同構的）時才存在。這樣的交結映射除了差一個乘法因子（K 中一個非零標量）是惟一的。這些性質當 K[G] 的像是具有中心 K_d 的單代數時成立（由所謂的舒爾引理：參見單模）。作為一個推論，在一些重要情形構造一個交結映射足夠證明表示同樣是有效的。