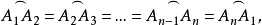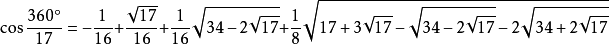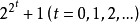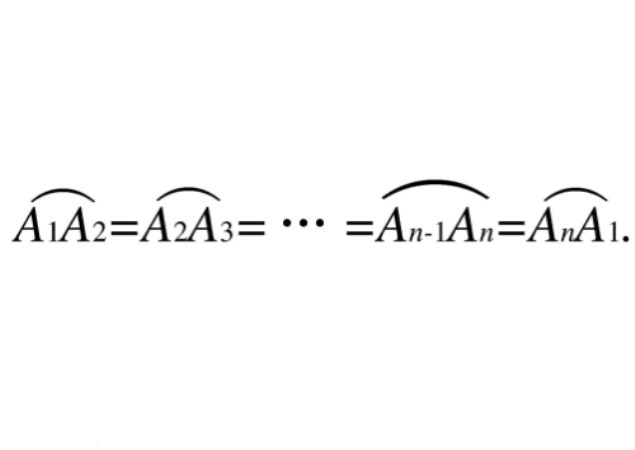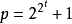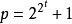等分圓周

等分圓周是指利用直尺和圓規將圓周n等分，這是一個古老的數學問題。古代希臘數學家利用尺規作圖可將圓周分成3，4，5，15等分，並進而將分點逐次倍增，將圓周無限等分。高斯(Gauss，1777-1855)曾證明可用尺規作圖將圓周17等分，因而找到了正十七邊形的尺規作圖法。為此，後人把這一圖形銘刻在高斯紀念碑上。

基本介紹

• 中文名：等分圓周
• 外文名：circumference in equal parts 
• 所屬學科：數學
• 所屬問題：平面幾何(圓)
• 相關人物：高斯(C.F.Gauss)
• 相關概念：費馬數

基本介紹

等分圓周(circumference in equal parts)是圓內接正多邊形的作圖問題。若圓周上依次有n個點A₁，A₂，A₃，…，A_n(n≥2)，把整個圓周分成n段相等的弧：

則稱點A₁，A₂，…，A_n把圓周n等分，簡稱n等分圓周。除二等分圓周外，用圓規直尺等分圓周與內接正多邊形的作圖實質是相同的問題。高斯(C.F.Gauss)對等分圓周曾做出巨大貢獻。1796年，年僅19歲的高斯根據式子

發現，圓內接正十七邊形可用圓規直尺作圖。1801年，高斯又研究確定用圓規直尺等分圓周，等分數所應滿足的充分必要條件(參見下文“用圓規直尺等分圓周問題”)，高斯臨終遺言“在墓碑上刻正十七邊形”，德國哥廷根大學為他建立了一座以正十七稜柱為底座的紀念像。

用圓規直尺等分圓周問題

用圓規直尺等分圓周問題是幾何學歷史中的一個著名問題，能僅用圓規直尺把圓周n等分，若且唯若n是如下形式的整數：

1.n=2^m(m為大於1的正整數)。

2.n=2^m·p₁·p₂·…·p_k，其中m=0，1，2，…，k=1，2，…，p_i為

型的不同素數，這是1801年高斯(C.F.Gauss)證明的，因此，在100以內可以用圓規直尺等分圓周的等分數只有24個：1型的五個為4，8，16，32，64；2型的十九個為3，6，12，24，48，96，5，10，20，40，80，15，30，60，17，34，68，51，85。在什麼條件下可以用圓規直尺等分圓周問題，自19世紀初葉被高斯解決以後，仍有許多數學家為此問題著迷。比較有趣的是

是素數時的情形，當t=0，1，2時，n=3，5，17的作圖法已經解決。當t=3，4時，n=257，65537，這兩個數都是素數，正257邊形的作圖，於1832年為里歇洛(F.J.Richelot)所完成；赫姆斯(P.Hermes)費了十年的時間才完成正65537邊形的作圖。關於費馬數

是否素數的探討參見“費馬數”。