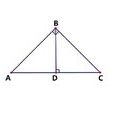
基本介紹
定義,驗證推導,定理推廣,面積射影定理,證明思路,提出者簡介,
定義
在△ABC中，設∠A，∠B，∠C的對邊分別為a，b，c，則有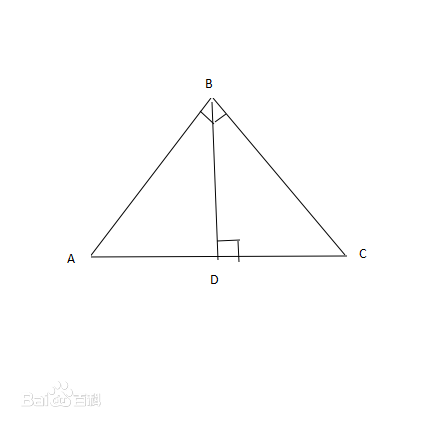
a=bcosC+ccosB b=ccosA+acosC c=acosB+bcosA |
這三個式子叫做射影定理。
驗證推導
①CD2=AD·BD;
②AC2=AD·AB;
③BC2=BD·AB;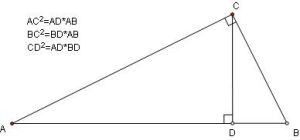
④AC·BC=AB·CD
證明：①∵CD2+AD2=AC2,CD2+BD2=BC2
∴2CD2+AD2+BD2=AC2+BC2
∴2CD2=AB2-AD2-BD2
∴2CD2=(AD+BD)2-AD2-BD2
∴2CD2=AD2+2AD·BD+BD2-AD2-BD2
∴2CD2=2AD·BD
∴CD2=AD·BD
②∵CD2=AD·BD(已證)
∴CD2+AD2=AD·BD+AD2
∴AC2=AD·(BD+AD)
∴AC2=AD·AB
③BC2=CD2+BD2
BC2=AD·BD+BD2
BC2=(AD+BD)·BD
BC2=AB·BD
∴BC2=AB·BD
④∵S△ACB=
AC×BC= AB·CD
∴ AC·BC= AB·CD
∴AC·BC=AB·CD
定理推廣
歐幾里得提出的面積射影定理projective theorem規定“平面圖形射影面積等於被射影圖形的面積乘以該圖形所在平面與射影面所夾角的餘弦。(即COSθ=S射影/S原）。”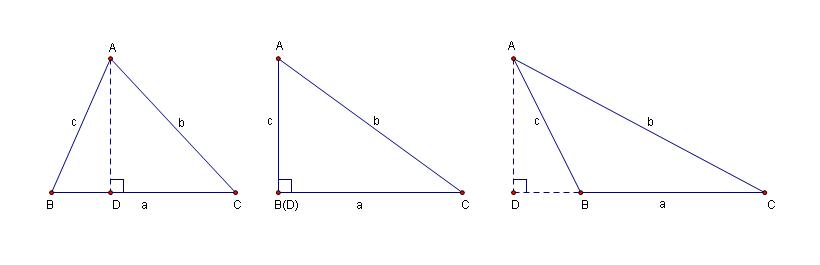
射影定理的推廣證明
射影定理的推廣證明在四面體A－BCD中，有 
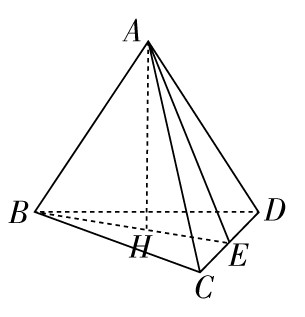
面積射影定理
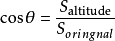
證明思路
因為射影就是將原圖形的長度（三角形中稱高）縮放，所以寬度是不變的，又因為平面多邊形的面積比=邊長的乘積比。所以就是圖形的長度（三角形中稱高）的比。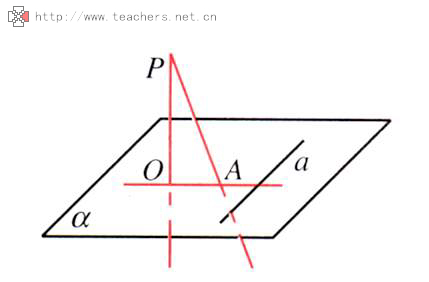
正射影二面角的歐幾里得射影面積公式
正射影二面角的歐幾里得射影面積公式那么這個比值應該是平面所成角的餘弦值。在兩平面中作一直角三角形，並使斜邊和一直角邊垂直於棱（即原多邊形圖的平面和射影平面的交線），則三角形的斜邊和另一直角邊就是其多邊形的長度比，即為平面多邊形的面積比。將此比值放到該平面中的三角形中去運算即可得證。
提出者簡介
歐幾里得（希臘文：Ευκλειδης ，公元前325年—公元前265年），古希臘數學家，被稱為“幾何之父”。他活躍於托勒密一世（公元前323年－公元前283年）時期的亞歷山大里亞。
直角三角形中的射影定理
直角三角形中的射影定理