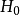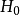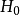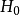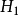第一類誤差，也稱為 α錯誤、“棄真”錯誤。是指在統計檢驗時，在原來的假設為真的情況下，作出了拒絕原假設的一種錯誤推斷。
基本介紹
- 中文名：第一類誤差
- 外文名：type I error
- 概念：原假設為真而拒絕原假設的錯誤
- 別名：“棄真”錯誤
- 隸屬：假設檢驗的一種錯誤
- 學科：數學
基本內容,產生原因,影響,兩類錯誤的關係,減少錯誤的方法,
基本內容
假設檢驗：事先對總體參數或分布形式作出某種假設，然後利用樣本信息來判斷原假設是否成立的過程。
假設檢驗的類型:統計假設一般可分為參數假設與非參數假設。參數假設是指總體分布類型已知，對未知參數的統計假設。檢驗參數假設問題成為參數檢驗。當總體分布類型為常態分配時，則為正態總體參數檢驗。非參數假設是指總體分布類型不明確，對參數的各種統計假設。檢驗非參數假設問題稱為非參數檢驗，也稱分布檢驗。
假設檢驗的特點:1、統計檢驗的假設是關於總體特徵的假設；2、用於檢驗的方法是以檢驗統計量的抽樣分布為理論根據的；3、作出的結論是機率性的，不是絕對的肯定或絕對的否定。
第二類錯誤（Ⅱ類錯誤）也稱為β錯誤，是指虛無假設錯誤時，反而接受虛無假設的情況。發生的機率為β。即沒有觀察到存在的處理效應。
產生原因
檢驗統計量是隨機變數， 有一定的波動性，在進行假設檢驗時，即使原假設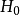
為真，而由樣本實驗數據計算的統計量值仍有一定的機率α落入拒絕域內，從而錯誤地拒絕原假設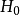。α為犯第一類錯誤的機率，稱為顯著性水平。1－α為當原假設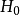為真而作出正確判斷的機率。α越小，犯第一類錯誤的機率就越小。第一類錯誤可能產生原因：1、樣本中極端數值。2、採用決策標準較寬鬆。
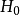
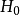
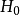
影響
犯Ⅰ類錯誤的影響較大，由於報告了本來不存在的現象，則因此現象而衍生出的後續研究、套用的危害將是不可估量的。相對而言，Ⅱ類錯誤的危害則相對較小，因為研究者如果對自己的假設很有信心，可能會重新設計實驗，再次來過，直到得到自己滿意的結果（但是如果對本就錯誤的觀點堅持的話，可能會演變成Ⅰ類錯誤）。
兩類錯誤的關係
1、 α+β不一定等於1。
2、在樣本容量確定的情況下，α與β不能同時增加或減少，而是此消彼長的關係。
減少錯誤的方法
在實際套用中，若水平α很小，原假設 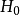不會輕易被否定． 如果樣本落入了否定域，作出“否定原假設 H0”的結論就比較可靠，此時犯第一類錯誤的機率很小。 反之，當 α 很小時，如果樣本落入了接受域，作出“接受原假設 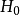”的結論就未必可靠，這只能表明: 在所選定的水平下沒有充分根據否定原假設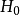，但絕不意味著有充分的根據說明它正確，因為此時犯第二類錯誤的機率可能很大。而在求解兩類錯誤機率大小的關鍵是明白接受域和拒絕域的具體內容，按條件機率的定義來求解。 而為了控制犯兩類錯誤的機率，通常有兩種方法: ①適當地增大樣本個數 n，理論上可行，在實際操作中不太可行。 ②限制犯第一類錯誤機率的原則，當樣本個數 n 確定後，在保證犯第一類錯誤的機率不超過指定數值α( 0 <α<1，通常取較小的數) 的檢驗中，尋找犯第二類錯誤機率儘可能小的檢驗。
