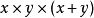公式,立方和公式,立方差公式,三項立方和公式,推導過程:,完全立方公式,分解步驟如下,解題時常用它的變形:,公式證明,疊代法一,疊代法二,排列組合法,因式分解證明,幾何驗證,
公式
立方和公式
立方差公式
三項立方和公式
推導過程:
立方和:
a3+b3
=a3+a2b-a2b+b3
=a2(a+b)-b(a2-b2)
=a2(a+b)-b(a+b)(a-b)
=(a+b)[a2-b(a-b)]
=(a+b)(a2-ab+b2)
立方差:
a3-b3
=a3-b3+a2b-a2b
=a2(a-b)+b(a2-b2)
=a2(a-b)+b(a+b)(a-b)
=[a2+b(a+b)](a-b)
=(a-b)(a2+ab+b2)
完全立方公式
分解步驟如下
(a+b)3=(a+b)(a+b)(a+b) = (a2+2ab+b2)(a+b)=a3+3a2b + 3ab2+ b3
解題時常用它的變形:
(a+b)3= a3+ b3+ 3ab(a+b) 和 a3+ b3= (a+b)3- 3ab(a+b)
(a-b)3=(a-b)(a-b)(a-b)=(a2-2ab+b2)(a-b)=a3-3a2b+3ab2-b3
立方和累加
公式證明
疊代法一
我們知道:
2次方和的求和公式
,即
——
平方和公式,此公式可由同種方法得出,取公式
,疊代即得。
具體如下:
(k+1)3 - k3 = (k3 + 3k2 + 3k + 1) - k3 = 3k2 + 3k + 1
利用上面這個式子有:
23 - 13 = 3×12 + 3×1 + 1
33 - 23 = 3×22 + 3×2 + 1
43 - 33 = 3×32 + 3×3 + 1
53 - 43 = 3×42 + 3×4 + 1
……
(n+1)3 - n3 = 3×n2 + 3n + 1
把上述各等式左右分別相加 得到:
(n+1)3-13 = 3×(12+22+32+……+n2) + 3×(1+2+3+……+n)+n×1
n3 + 3n2 + 3n + 1 - 1 = 3×(12+22+32+……+n2)+3×n(n+1)/2+n (1)
其中12 + 22 + 32 + …… + n2 = n(n+1)(2n+1)/6
代入(1)式,整理後得 13 + 23 + 33 + …… + n3=[n(n+1)/2]2
疊代法二
那么就得出:
…………
於是⑴+⑵+⑶+…+(n)有
把以上這已經證得的三個公式代入,
即
推導完畢。
排列組合法
設數列{
}=n(n+1)(n+2),其n項和為
,且設
=
+
+
+…+
,則
=1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
又
=1×(1+1)×(1+2)+2×(2+1)×(2+2)+…+n(n+1)(n+2)
=…
因式分解證明
幾何驗證
透過繪立體的圖像,也可驗證立方和。根據右圖,設兩個立方,總和為:
 圖象化立方和公式
圖象化立方和公式把兩個立方體對角貼在一起,根據虛線,可間接得到:
要得到
,可使用
的空白位置。該空白位置可分割為3個部分:
把三個部分加在一起,便得:
之後,把
減去它,便得:
公式發現兩個數項皆有一個公因子,把它抽出,並得:












































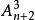


























 圖象化立方和公式
圖象化立方和公式